|
Related Links:
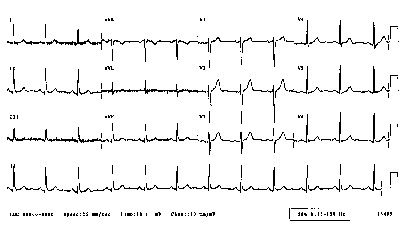
CAST, SWORD, Guarded Receptors, Vulnerability, Ventricular Fibrillation, Spiral Waves and Sudden Cardiac DeathSudden death arises from disturbances in the regular excitation of the heart. Mostly, disturbances in the regular rhythm arise from either premature excitation or by breaking an excitation wave as it collides with either an obstacle, a region of reduced excitability or another wave. A heart is always vulnerable to disturbances in the regular excitation process. BY vulnerable, I mean that premature excitation can lead to replacing the normal SA-node driven excitation to sustained reentrant excitation - that can lead to atrial or ventricular fibrillation. Vulnerability occurs when there is an asymmetry of tissue excitablity, caused either by the passage of a previous wave or by the anisotropic nature of coupling between cells. Vulnerability can be amplified by reducing the excitability of the heart, i. e. shifting the excitability closer to the boundary between excitable and refractory. When the heart beats regularly, the electrocardiogram reveals a regular pattern of changes in potential as shown here.
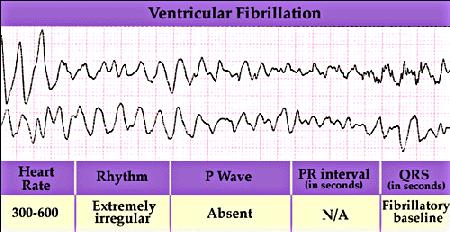
 However, when the heart is in a vulnerable state, then the regular pattern of excitation of the heart can be interrupted by a premature excitation leading to a reentrant arrhythmia. All to often the wavefront associated with the premature excitation is not completely formed (i.e. continuous), but broken and the ends of the broken front begin to curl, signaling the formation of a spiral wave. Depending on the excitability of the heart, the spiral wave will rotate around a stationary core or will meander. If the spiral wave breaks and forms additional spirals, then the heart will no longer be stimulated in a regular manner, but in an irregular manner - with different regions of the heart excited asynchronously. The result is an electrocardiogram that reveals non-repetitive activation as shown here.
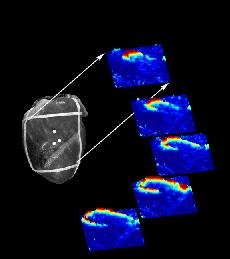
Voltage sensitive optical dyes reveal the spiral nature of wave motion in the heart as shown here (from Art Winfree's site).
Notes - Nov 2003A propagating wave of excitation in the heart can be broken (a precursor of spiral wave formation) by manipulating the excitability of the heart. The excitability can be altered by drugs, by decouping cells, by ischemic regions and by premature excitation. A wave propagating in a region that contain regions of excitable and regions of unexcitable tissue will be broken. Because there are more unexcited cells adjacent to the ends of a front than adjacent to cells within the front, the ends travel slower (due to the fact that an excited cell has a limited amount of charge available to excite neighboring cells). This results in curling of the ends and the formation of a spiral wave. I have explore several conditions associated with altering excitability, including genetic alteration of the Na channel and class I antiarrhythmic drugs. Earlier, we explore breaking waves with obstacles. Here are links to these papers.
Studies of the relationship between excitability, spiral wave stability and spiral wave fragmentation were described here
My curiosity about the relationship between vulnerability and altered excitability was triggered by our observation that often substance abusers appear in emergency rooms with cardiac tachyarrhythmias. We found that most abused substances, cocaine, tricyclic antidepressants, darvon (propoxyphene) all are use-dependent Na channel blockers. Here was our initial observation This triggered an intense investigation of the theoretical mechanism of cardiac vulnerability and experimental verification. Below are key papers that reveal the theory and experimental verification in both cardiac tissue and in the Belousov-Zhabotinsky excitable chemical medium.
Recent notes - March 2001This is a story about how to start potentially fatal heart rhythms (or rather, the absence of a regular rhythm). The story begins with an impulse that starts a cascade of cellular activation and an unexpected impulse, that can initiate an activation sequence leading to fibrillation and sudden cardiac death. The focus below is to outline the ideas thought to underlie initiatiation of potentially fatal arrhythmias - particularly unexpected impulses that fall within the vulnerable period. In the late 80s, we showed that many antiarrhythmic drugs extended this interval of vulnerability - but we did not understand physical mechanism responsible for this association. Over the years, additional data, additional numerical studies and then this year (2001), the pieces finally fit together. Our ideas are sufficiently well developed that we can describe the physics of arrhythmia initiation - and link drug properties to this physical model. One recent addition, this year: - with these, we outline the link between drug unbinding which controls the gradient of excitability trailing an activation wavefront. These are the missing links from our story that started 10 years ago.
1991-1998: Original Ideas - slightly stale, but still useful history
 
The CAST and the SWORD Several large clinical trials (CAST and SWORD) failed to show that frequenly used antiarrhythmic drugs could actually reduce the rate of sudden cardiac death. To the contrary - they demonstrated a 2x to 3x increase in the rate of sudden cardiac death. For the past 20 years, Gus Grant and I have been studying - at the single channel and whole cell level, the interaction of antiarrhythmic drugs with membrane ion channels. We developed a simple model of drug interaction with ion channels, the guarded receptor model, and verified it with numerous experiments (see bibliography). With Maddy Spach, we have explored the role of propagation in wavefront formation and with Josef Starobin, we have developed an accurate model of front formation. Together, these results revealed a previously unknown feature of use-dependent ion channel blockade - prolongation of the cardiac vulnerable period . Recent studies by us in rabbit atrial tissue confirmed these hypotheses.



The guard and another guard - protecting the channel
In mid 1996, Art Winfree invited me to write a tutorial for the January 98 issue of Chaos - about how drugs (Class I (Na channel blockers) and III ( K channel blockers) antiarrhythmic drugs) can increase the likelihood of Sudden Cardiac Death. The manuscript never made it to publication, for a variety of reasons. But, rather than sit of the results, I have decided to outline the main ideas here - mostly as an experiment to explore the possibility to makes these results web-accessible. The primary purpose for this manuscript was to review the basic mechanisms associated with wave fragment formation - in the setting of supposedly antiarrhythmic drugs. What we uncovered was that all Class I antiarrhythmic drugs significantly extend the Vulnerable Period, the interval during which premature stimulation leads to wave fragmentation and spiral formation. Moreover, the degree of prolongation is directly proportional to the unbinding rate constant of the drug. So the guarded receptor model of drug-channel blockade provides a direct mechanism for assessing the rates of blocking and unblocking, from which the proarrhythmic potential can be computed. The main result is that any agent that extends the refractory period by Na channel blockade will INCREASE the vulnerable period. Thus the "antiarrhythmic" mechanism for suppressing PVC, in fact is also a proarrhythmic mechanism for increasing the likelihood that an unsuppressed VPC will initiate wave fragmentation, spiral formation and progression to ventricular fibrillation and SUDDEN CARDIAC DEATH. 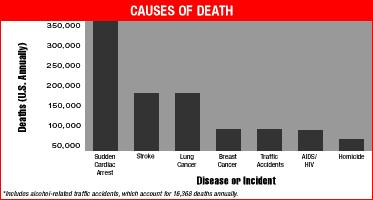 
Sudden Death ?
Recently Valentine Krinsky invited me to revisit this manuscript. Its amazing what 4 years of fermentation can do to ideas - and I realized that as much as it pains me, some of the earlier criticism from Art was justified. So I set about resolving some areas of ambiguity, and decided the best place for this was Pushchino. So, the day after Thanksgiving, 2000, I was off to see my colleagues in Pushchino and to have 2 or 3 weeks of peace and quiet in order to sort out this manuscript. The first reading (after 4 years) was the realization that 1 paper = 1 idea , and this paper had too many ideas. So I extracted everything except the work on the vulnerable period and then realized that there was a big missing chunck of insight - why was the use-dependent VP > reduced gNa VP given the same conduction velocity. The result is was a much better paper and maybe even Art would agree. For those wishing for a contemporary view of Pushchino life, visit here To my knowledge, the basic ideas outlined below are correct (after all the ideas are motivated by the physics of drug-channel interactions, and the physics of wave formation and propagation) and applicable to clinical trials of drugs that block ion channels. The main idea is that arrhythmias start by either a group of cells that decide to spontaneously oscillate - or by creating wave fragments. Wave fragmentation can occur spontaneously (at least in models - see Alain Karma's work: Phys Rev Lett 71:1103-1106, 1993 Spiral Breakup in Model Equations of Action Potential Propagation in Cardia Tissue), by wave-obstacle collisions (see Kostya Agladze's paper in Science 264:1746-1748, 1994; Rotating spiral waves created by geometry; or Starobin and Starmer, Phys Rev E 54:430-437, 1996; Boundary-layer analysis of waves propagating in an excitable medium: medium conditions for wave-front-obstacle separation ) or by stimulation within the vulnerable period (Starobin, Zilberter and Starmer, Physica D 70:321-341, 1994 - Vulnerability in one-dimensional excitable media). Here we focus on the VP - and its extension by "anti-arrhythmic" drugs. The drug model was proposed by our group in 1983 ( Starmer, C.F. and Grant, A.O. Phasic ion channel blockade: A kinetic model and method for parameter estimation. Molecular Pharmacology 28:348-356, 1985) and has since been validated by a large number of groups ( see for instance - Starmer, C.F., Yeh, J.Z. and Tanguy, J. A quantitative description of QX222 blockade of sodium channels in squid giant axon. Biophysical J. 49:913-920, 1986; Gilliam, F.R., Starmer, C.F. and Grant, A.O. Blockade of rabbit atrial sodium channels by lidocaine: characterization of continuous and frequency-dependent blockade. Circulation Research 65:723-739, 1989; Whitcomb, D.C., Gilliam, F.R., Starmer, C.F. and Grant, A.O. Marked QRS complex abnormalities and sodium channel blockade by propoxyphene reversed with lidocaine. Journal of Clinical Investigation 84:1629-1636, 1989). The vulnerable period was described by Art Winfree in "When Time Breaks Down" and studied numerically by us in the setting of use-dependent drugs (Starmer, C.F., Lastra, A.A., Nesterenko, V.V. and Grant, A.O. A proarrhythmic response to sodium channel blockade: Theoretical model and numerical experiments. Circulation 84:1364-1377, 1991. Starmer, C.F., Biktashev, V.N., Romashko, D.N., Stepanov, M.R., Makarova, O.N. and Krinsky, V.I. Vulnerability in homogeneous excitable media: Analytical and numerical studies of unidirectional propagation, Biophysical Journal, 65:1775-1787, 1993). As a result of conversations between me and Vicente Perez-Munuzuri, Vicente's group explored vulnerability experimentally in the BZ medium ( Gomez-Gesteira, M., Fernandex-Garcia, G., Munuzuri, A.P., Perez-Munuzuri, V, Krinsky, V.I., Starmer, C.F. and Perez-Villar, V. Vulnerability in excitable Belousov-Zhabotinaky medium: From 1D to 2D. Physica D 76:359-368, 1994) and more recently we propsed theoretical framework: (Starobin, J., Zilberter, Y.I. and Starmer, C.F. Vulnerability in one-diensional excitable media, Physica D 70:321-341, 1994. ) In addition, we experimentally verified the modulation of the vulnerable period by Na channel blockers in 1992 (Starmer, C.F., Lancaster, A.R., Lastra, A.A. and Grant. A.O. Cardiac instability amplified by use-dependent Na channel blockade. American Journal of Physiology 262:H1305-H1310, 1992; Nesterenko, V.V., Lastra, A.A., Rosenshtraukh, L.V. and Starmer, C.F. A proarrhythmic response to sodium channel blockade: The influence of antiarrhythmic drugs on the window of vulnerability in guinea-pig myocardium. Journal of Cardiovascular Pharmacology 19:810-820, 1992). One reviewer found our hypothesis overly simplistic, an interesting observation in light of experimental verification of all the ideas discussed below.
Cellular Responses to Na Channel BlockadeAs shown below, normally a cardiac cell responds to stimulation by switching its membrane potential (Vm), generating anaction potential. Because the time constant of recovery from Na channel inactivation (h and j) is much longer than the time constant of recovery of activaiton (m), there is a refractory period - as illustrated. The cell is unexcitable until the membrane potential has returned to the rest potnetial as shown below. 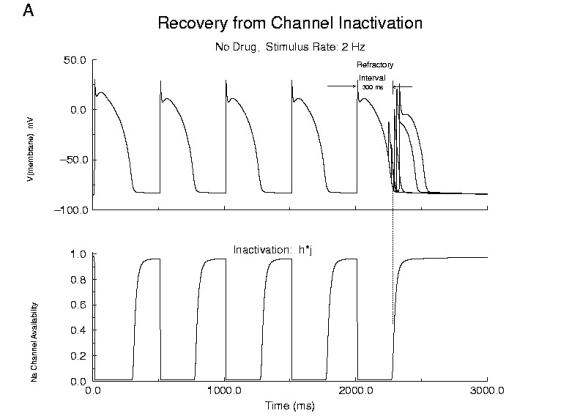 Refractor Period Without Drug When one blocks Na channels, particularly with use-dependent drugs, the refractory period is prolonged, a reflection of the slow unbinding rate of dissociation of drug from the channel receptor. Most Class I antiarrhythmics are use-dependent - and selectively bind to either open or inactivated channels - and when the channel is not in a bindable conformation - the drug unbinding time constant is prolonged - thus prolonging the refractory period as shown here.
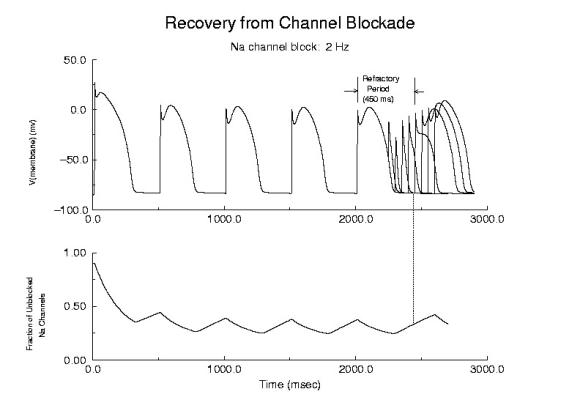 Prolonged Refractory Period With Class I Drugs Because of the use-dependent nature of channel blockade, membrane responses are sensitive to stimulation rate as shown here - where the stimulation rate is is sufficiently rapid that the refractory period is extended into the time of the next stimulus - thus producing an alternating pattern of cellular responses as shown here. 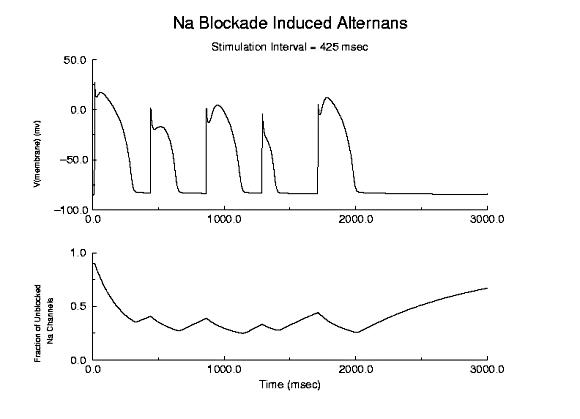 Alternans
A Model of the Cardiac Vulnerable PeriodThe cardiac vulnerable period has long been a difficult concept to visualize. If you assume a uniform medium then the critical question is how to start a reentrant wave of activation. In mathematical terms, how to create a phase singularity. In many textbooks, one finds a triangle of conducting tissue - where one leg of the triangle is transiently refractory - due to prior stimulation. This model requires inhomogeneities in refractory properties which certainly exist in cardiac tissue, but such inhomogeneities are unnecessary as shown below. Specifically Wiener showed that in any system with a traveling refractory tail, it is possible (in 2 dimensional medium) to create a phase singularity by stimulating in the region where the media excitabilty changes from non-excitable (due to the refractory state) and excitable (caused by slightly longer time for the refractory state to switch to a rest state). Because there is a critical liminal region that must be excited in order for any wave to successly propagate, there is a time, when the stimulus field spans the transition from non-excitable to excitable - thus resulting in a wave the cannot propagate in some directions and can propagate in other directions as shown below. Art Winfree drew a picture of this process in "When Time Breaks Down" and gave meat to the Weiner skeleton. Because a finite interval of time is required for the critical point to traverse the suprathreshold region of the stimulus field, there is a finite period of vulnerability which can be approximated by VP = (L - Lliminal)/v.
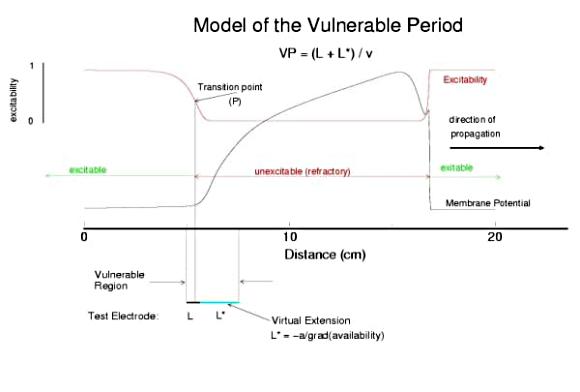
Vulnerable Period Model Shown here is an action potential propagating along a cable, from left to right (top). Also shown is the front of inactivation (top). At rest, the tissue is fully excitable, and virtually all cells are available for conduction (not inactivated). Upon excitation, channels become inactivated and the cells are transiently unexcitable. At the bottom of the figure is the electric field generated by a stimulating electrode. Note that the field decays exponentially on either side of the site. The middle region of the field is above the stimulation threshold while the region more perpherial is sub-threshold. Now, the critical point is to understand that as the cell recovers from channel inactivation, there is a critical point where medium to the left if excitable and medium to the right is not excitable. When this point falls within the suprathreshold region of the stimulation field, a wave will propagate retrograde (away from the initial wave) and fail to propagate toward the initial wave (antegrade). Clearly, if the cable ends were joined, then this wave would circulate. In fact, in 2D and 3D, such partially propagating waves evolve into spiral waves that reflect the main features of a reentrant cardiac arrhythmia. The duration of the vulnerable period is determined by the time the critical point, P, to pass through the suprathreshold stimulus region. The vp can be approximated by VP = (L - Lliminal)/v where L is the length of the suprathreshold region and v is the velocity of the conditioning wave. Thus anything that slows propagation is proarrhythmic and increases the period of vulnerability. However, the use-dependent properties of Class I drugs further amplify the vp because of drug-uptake during the time of front formation following premature stimulation. We indicate above, the virtual electrode extension, required to increase the excitability sufficient to support establishing stable wave motion. The boundaries of the vulnerable period can be readily demonstrated with numerical experiments. Here are 5 ms snapshots of the spatial distritution of the membrane potential, showing the tail of the conditioning wave (traveling from left to right) and the responses to test stimuli. Demonstration of the Cardiac Vulnerable Period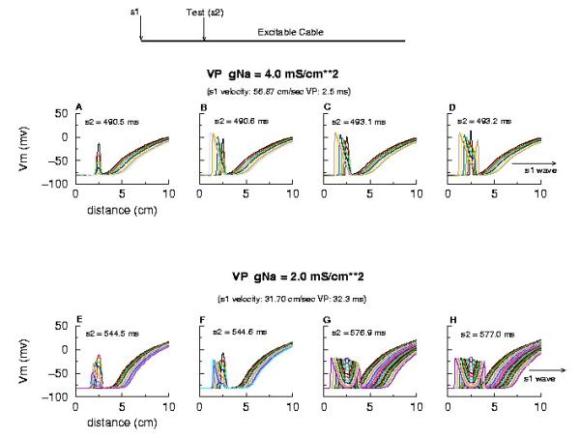 Vulnerable Period without Drug Here,note that reducing gNa slows propagation and thus slows the time required for the critical point, P, to pass through the suprathreshold region - in concert with VP = L/v. However there is something quite interesting happening. Note the time required to establish stable propagation at the uni-bi directional conduction boundary. For gNa = 4.0, only 10 - 15 ms are required - whereas for gNa = 2.0, near the threshold of propagation, more than 50 ms are required. This suggests that the VP is not only dependent on the velocity of the conditioning wave, but also on the gradient of excitability at the s2 stimulation site.
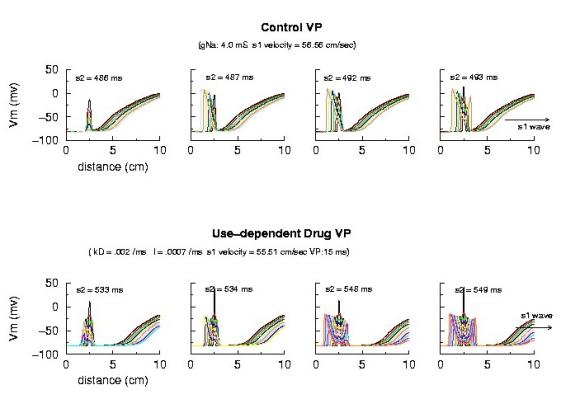 Vulnerable Period Boundaries with Drug Here, the effect of conduction velocity is factored out of the experiment - by introducing a test stimulus immediately after the passage of the first conditioning wave. Because the initial conditions were set at zero blockade, the conduction velocity of the conditioning wave was essentially that of the drug-free experiment. Shown above is an increase in the VP from 5 ms to 15 ms - with the same conduction velocity. Where did the additional VP extension come from? My current hypothesis is that this is the result of the small gNa gradient at the s2 test site - and thus, the time required to establish stable propagation is much longer than in the drug-free situation. Thus, antiarrhytymic drugs are double-edged agents - they are supposedly antiarrhythmic by suppressing excitability, but are proarrhythmic by slowing conduction AND extending the time required for stable propagation to develop. Not a good situation. This effect can be readily appreciated below. Note that the VP vs 1/v relationship is linear for both gNa changes and for use-dependent drug. The drug line, though, is offset by approximatly 15 ms - the time required (for this drug) to develop stable propagation. I've been puzzled by this graph ever sense I made it 12 years ago - and finally noticed the effect on the left side of the time plots of front develoopment (above). I'm a slow learner!
So - is this model of vulnerability real? How to test the idea. IF its correct, then it should be possible to identify the critical point, P, as the common intersection of Na channel availability, for different availability conditions - and the simplest is to change GNa - the maximum sodium channel conductance. Below is a trace of the availability (top) and the action potential, at the bottom - demonstrating a common intersection of availability - associated with the transition from block to uni-directional conduction. (The scale for channel availability is 15x, and the membrane potential traces are at 5 ms intervals (at the s2 site) - the tails are from individual action potentials and I apologize for the complexity).
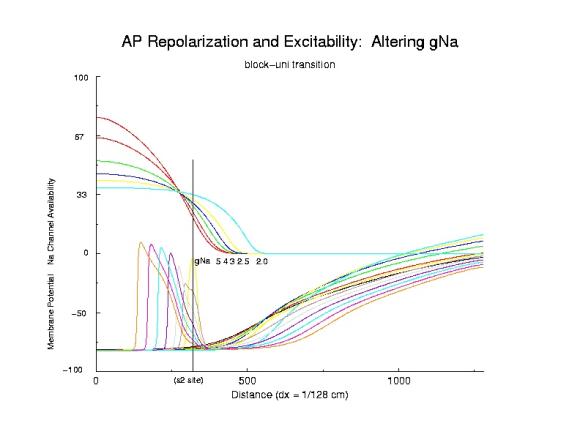 Identifying the critical Na channel availability
Role of availability gradient in front formationHere we show the role of the availability gradient on the formation time of the antegrade wave. Shown are 2 conductances: 5 (control) and 2 (marginally excitable). Each trace of the propagating action potential is a snapshot of the spatial membrane potential distribution, taken every 5 ms. Note the slow process of stable propagation for the marginally excitable medium, coupled with slow propagation - while for the normal Na channel availability, s2 antegrade front formation is rapid and propagation is fast.
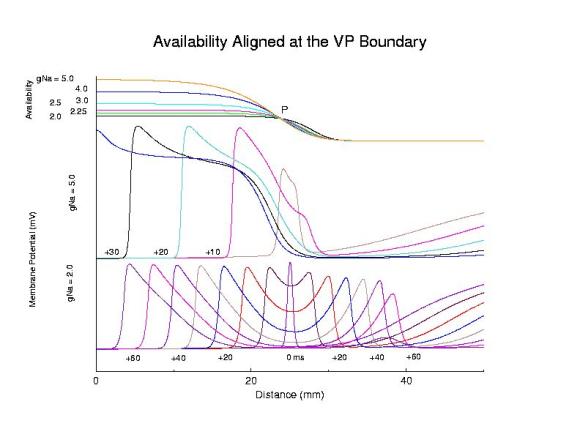
Comparing steep and shallow gradient effects on front formation
The distance that the critical point, P, must travel in order to produce a stable antegrade wave, extends the vulnerable region, and is the major determinant of the danger in slowly unbinding Class 1 antiarrhythmics. From a mechanistic point of view, the class 1 antiarrhythmics with the slowest unbinding process appears to be the open channel blockers, where the drug is trapped within the channel during the diastolic interval. This extension of the vulnerable region accounts for the upward shift in the VP - 1/velocity relationship displayed below
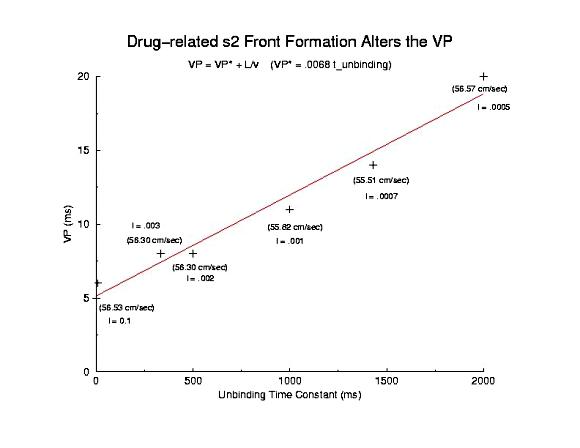
Summary of Use-Dependent Drug Extension of the Cardiac VP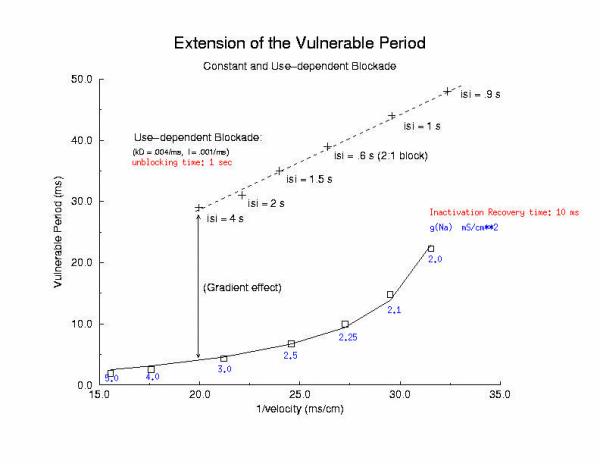 Summary Results Here I plot the vulnerable period for for different values of gNa (continuous blockade) and for different stimulus intervals of a use-dependent drug - as a function of the reciprocal conduction velocity. Our theory predits a linear relationship between vp and 1/velocity - and this was observed in our numerical experiments with use-dependent blockade, but not for continuous blockade. What is very interesting is that for the same conduction velocity, we observed a dramatic increase in the vp for use-dependent drugs over that associated with a simple reduction in gNa (secondary to depolarizing the rest potential or a reduced expression of Na channels). Why? - it seems that there is a very interesting interaction between drug uptake during formation of the front initiated by premature stimulation - that results in additional prolongation of the vp. Perhaps this is significant with respect to the CAST study? - I am working on this problem (as we speak) and the work above, demonstrating the variation in front formation time, as a function of channel availability (and its gradient) seems relevant. Here, we confirm the gradient effect on the VP extension by exploring the VP following the first conditioning pulse, and varying the unbinding rate constant for a use-dependent channel blocking agent. Note the linear extension with the unbinding rate. This is easy to see with a little algebra. The gradient of availability, after inactivation recovery is d gNa*(1-b)/dx and, from the model of ion channel blockade: db/dt = kD(1-h)(1-b) - lb. Because the channel binding sites are inaccessible at the rest potential, the association term drops out and so db/dt = -lb an unbinding process. Now gNa*(1-b) must cross the critical value - so its possible to compare the gradients simply by realizing the the unbinding rate constant is proportional to the derivative (db/dt) - since b is determined by the critical point P - and is independent of the maximum conductance. Thus the gradient is -db/dt / dx/dt or -1/v db/dt = - "el"/v. The inverse gradient, thus is proportional to 1 / db/dt is the reciprocal rate constant, l. The time constant of unbinding, t is 1/l. Here we plot the unbinding time constant against the VP and see a reasonably nice linear fit. This linear relationship is quite reassuring, given all the assumptions required to extimate the gradient.
 Now, if you fully understand drug effects and the vulnerable period, its time to see what happens when you stimulate within the vulnerable region following a conditioning wave. Here is an aged link to some notes where I explored initiating spiral waves within the VP in FHN medium and then in the Beeler Reuter cardiac medium. The BR clips include the computed ECG which shows the transition from monomorphic to polymorphic configurations, following the transition from a stable circular core to an unstable, meandering of the spiral tip. The physics of this was discovered by Josef Starobin and described in our papers in Phys Rev E. |