



Next: Algebraic Models
Up: Taylor Series
Previous: Taylor Series
Index
Click for printer friendely version of this HowTo
Sometimes you are faced with an equation that appears to be a guess
by someone. Is there a way to figure out what it approximates? This
is particularly true with difference equations when someone is
approximating an ordinary differential equation or a partial differential
equation and they state a bunch of difference equations and one looks a bit
spooky. So here is a way to reverse engineer what is happening.
Typically, the equations involve a function and a couple of points, say
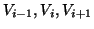 Now lets expand the function, V, around
point i as
Now lets expand the function, V, around
point i as
Now some preliminaries. Suppose we use
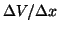 to approximate
a derivative. We see immediately form above that
to approximate
a derivative. We see immediately form above that
which shows that we estimate the left derivative with an error that is
proportional to the 2nd derivative. To get a sort of unbiased estimator
of the derivative - subtract equation 4 from 5 and you see:
or
Now this is a nice estimator - Note that dividing each side by
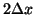 gives a
perfect approximation of the derivative - i.e. the higher order terms
disappear!
gives a
perfect approximation of the derivative - i.e. the higher order terms
disappear!
Now let's say that someone uses the difference equation
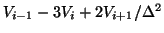 and we would like to know what it estimates. So we multiply equation 5 by 2
and add them getting
and we would like to know what it estimates. So we multiply equation 5 by 2
and add them getting
so moving the 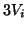 to the left we have
to the left we have
The paper where this appeared stated that the above difference equation
approximated the first derivative - and its obvious that it approximates a bit
more than the simple first derivative.




Next: Algebraic Models
Up: Taylor Series
Previous: Taylor Series
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19