


Next: Examples of Models
Up: Implicit Models
Previous: Implicit Models
Index
Click for printer friendely version of this HowTo
Also known as Quasi-Steady-State, this assumption allows you to model
a small portion of an extremely complex system. Simply put, without
this assumption many models would not exist and it allows us to work
with a system that has both fast and slow reactions. If you are
interested in the portion of the model that contains the slow, or rate
limiting reactions, you can
(sometimes) assume that the fast reactions are in a state of dynamic
equilibrium, and the their derivatives are equal to zero, compared to
the slow reactions. If you are interested
in the portion of the model that has fast reactions, you can assme
that the the slow portion does not change significantly (and thus,
it's deriviatve is zero) when compared to the fast.
Focus On Slow Reactionsno_title
For me, in the drug binding business, the channel
switches from closed to open and then it can be bound. The binding
reaction is slow and the channel transitions are fast. so C <===> O
<===> B
Now
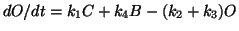 (1,2 are forward and revers
for C-O and 3,4 and forward and reverse for O-B.
(1,2 are forward and revers
for C-O and 3,4 and forward and reverse for O-B.
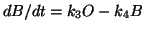
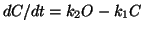 but this is fast compared with the others so lets
assume that it is always in equilibrium:
but this is fast compared with the others so lets
assume that it is always in equilibrium:
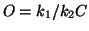 and then using
and then using
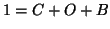 , you know that
, you know that
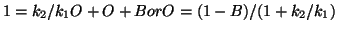 and now you can sumstitute into the dB/dt equation for O and solve for B
in terms of everything else.
and now you can sumstitute into the dB/dt equation for O and solve for B
in terms of everything else.
Focus On Fast Reactionsno_title
If we were interested in some intracellular process that required
external stimulation, we can often assume that the internal processes
are much faster than the externeral ones due to the fact that the
concentrations of the various players in the reactions are much higher
internally.



Next: Examples of Models
Up: Implicit Models
Previous: Implicit Models
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19