|
|




Next: Separation of Variables
Up: Methods for Solving ODEs
Previous: Methods for Solving ODEs
Index
Click for printer friendely version of this HowTo
Graphical Solutions: Phase Plane Analysis
Oftentimes we can gather a good deal of qualitative information about
a solution
to a differential equation without going through the trouble of
finding an analytic or numerical solution. Instead, we can simply
look for equilibrium points, or points where the derivative is zero,
and determine whether the function moves toward or away from these
points as time passes giving us the asymptotic behavior of the
function without having to solve for it.
One Stable Pointno_title
Consider the differential equation:
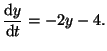 |
(2.10.1) |
When
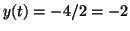 , ,
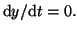 Thus, if Thus, if 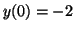 , then for any value of , then for any value of 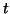 , , 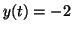 , since the derivative
will always be
zero. Thus , since the derivative
will always be
zero. Thus 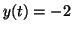 is called an equilibrium since it will not
change. However if is called an equilibrium since it will not
change. However if 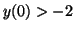 , then the derivative will be negative,
and
thus, as , then the derivative will be negative,
and
thus, as 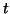 grows larger and larger, grows larger and larger, 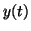 will converge to will converge to 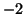 .
This is easily seen by simply plugging in different values for .
This is easily seen by simply plugging in different values for 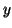 that are greater than
that are greater than 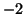 . For example, if . For example, if 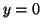 , then , then
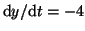 . If . If 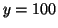 , then , then
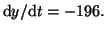 Likewise, if
Likewise, if 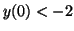 , than the derivative will be positive for all values of , than the derivative will be positive for all values of
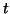 and and 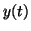 will approach will approach 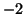 from below as from below as 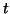 goes to infinity.
Since the line goes to infinity.
Since the line 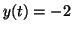 is approached from above when is approached from above when 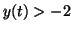 and below when
and below when 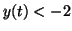 , it is called a node or a
stable state. This is because small perturbations to the
system at this point will only lead back to it. That is, if the
system is at , it is called a node or a
stable state. This is because small perturbations to the
system at this point will only lead back to it. That is, if the
system is at 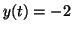 and some outside force knocks it to and some outside force knocks it to
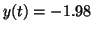 or or
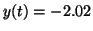 , it will asymptotically return to , it will asymptotically return to 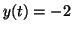 . .
Figure 2.10.1 shows an actual plot of the phase lines, or
slopes for various values of 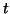 and and 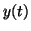 . Due to the fact that
there are no free instances of . Due to the fact that
there are no free instances of 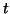 in Equation 2.10.1,
the slopes are the same for each value of in Equation 2.10.1,
the slopes are the same for each value of 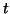 . In this illustration, it
is easy to see the stable point . In this illustration, it
is easy to see the stable point 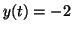 and how the slope of any
point above or below this line points toward it. Figure
2.10.2 demonstrates how that regardless of the initial
condition, as and how the slope of any
point above or below this line points toward it. Figure
2.10.2 demonstrates how that regardless of the initial
condition, as  gets larger, the solution will converge on the
stable equilibrium. Figure 2.10.3 shows how a
nullcline graph represents the same information. gets larger, the solution will converge on the
stable equilibrium. Figure 2.10.3 shows how a
nullcline graph represents the same information.
Figure:
A Phase Plot for Equation
2.10.1. There is a single, stable equilibrium at
 . .
![\includegraphics[height=3in,width=3in]{first_deq}](img335.png) |
Figure:
A Phase plane for Equation
2.10.1, with the solutions for the initial conditions,
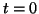 , , 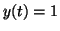 and and 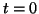 , , 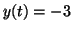 . Notice how, regardless of
whether or not the initial condition puts . Notice how, regardless of
whether or not the initial condition puts 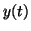 above or below the
stable equilibrium, as above or below the
stable equilibrium, as 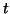 grows, they both converge to it. grows, they both converge to it.
![\includegraphics[height=3in,width=3in]{first_deq_init}](img336.png) |
Figure:
A nullcline for Equation
2.10.1. When 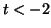 , the derivative
is positive. When , the derivative
is positive. When 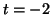 , the derivative is zero, and thus, this
is an equilibrium point. For , the derivative is zero, and thus, this
is an equilibrium point. For 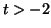 , the derivative is negative. Since the derivative is positive on
the left and negative on the right, , the derivative is negative. Since the derivative is positive on
the left and negative on the right, 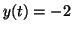 is a stable equilibrium is a stable equilibrium
![\includegraphics[height=3in,width=3in]{first_deq_nullcline}](img337.png) |
1 Stable and 2 Unstableno_title
Consider the cubic differential equation:
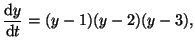 |
(2.10.2) |
where
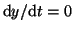 when when 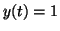 , , 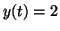 and and
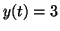 . By plugging in different values for . By plugging in different values for 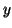 , we can
determine the slope at different points. In this case, we end up with
one stable point, , we can
determine the slope at different points. In this case, we end up with
one stable point, 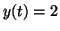 and two unstable points, and two unstable points, 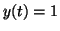 and and 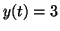 . By unstable, we mean
that if the system is at . By unstable, we mean
that if the system is at 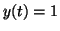 or or 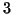 , and it is perturbed slightly, it
will not return to its original state. Instead, it will either move
toward , and it is perturbed slightly, it
will not return to its original state. Instead, it will either move
toward 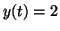 or or
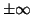 . This is illustrated in Figure
2.10.4.
Figure 2.10.5 shows the equivalent phase information
contained in a plot of the nullcline.
When the initial conditions are known, specific
solutions can be plotted and this is shown in Figure 2.10.6. . This is illustrated in Figure
2.10.4.
Figure 2.10.5 shows the equivalent phase information
contained in a plot of the nullcline.
When the initial conditions are known, specific
solutions can be plotted and this is shown in Figure 2.10.6.
Figure:
A Phase plane for Equation 2.10.2,
equilibria at 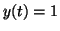 , , 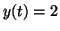 and and 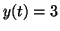 . The equilibrium at . The equilibrium at
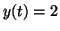 is stable since the slopes immediately above and below it
converge to it. is stable since the slopes immediately above and below it
converge to it.
![\includegraphics[height=3in,width=3in]{2nd_all_neg}](img342.png) |
Figure:
A nullcline for Equation 2.10.2.
There is one stable equilibrium at 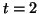 , where the derivative to
the left is positive and the derivative on the right is negative.
The other two equilibria are unstable. , where the derivative to
the left is positive and the derivative on the right is negative.
The other two equilibria are unstable.
![\includegraphics[height=3in,width=3in]{2nd_all_neg_nullcline}](img343.png) |
Figure:
A Phase plane for Equation 2.10.2,
with solutions with the initial conditions set to
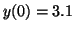 , ,
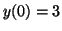 , ,
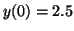 , ,
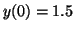 and and
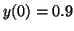 . Notice how
even though . Notice how
even though 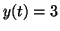 is an unstable equilibrium, and thus,
solutions will not converge on it, if that is where your solution
begins, it will not deviate from it without some other force acting
on it. is an unstable equilibrium, and thus,
solutions will not converge on it, if that is where your solution
begins, it will not deviate from it without some other force acting
on it.
![\includegraphics[height=3in,width=3in]{2nd_all_neg_init}](img344.png) |
2 Stable and 1 Unstableno_title
Consider the cubic differential equation:
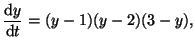 |
(2.10.3) |
where
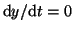 when when 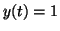 , , 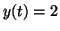 and and
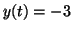 . Again, by plugging in different values for . Again, by plugging in different values for 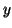 , we can
determine the slope at different points. In this case, we end up with
two stable points and one unstable point. This is illustrated in
Figure 2.10.7. , we can
determine the slope at different points. In this case, we end up with
two stable points and one unstable point. This is illustrated in
Figure 2.10.7.
Figure:
A Phase Plane for Equation 2.10.3.
There are two stable equilibria at 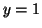 and and 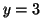 and an unstable
equilibrium at and an unstable
equilibrium at 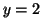 . .
![\includegraphics[height=3in,width=3in]{two_stables}](img346.png) |




Next: Separation of Variables
Up: Methods for Solving ODEs
Previous: Methods for Solving ODEs
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |
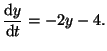
![\includegraphics[height=3in,width=3in]{first_deq}](img335.png)
![\includegraphics[height=3in,width=3in]{first_deq_init}](img336.png)
![\includegraphics[height=3in,width=3in]{first_deq_nullcline}](img337.png)
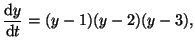
![\includegraphics[height=3in,width=3in]{2nd_all_neg}](img342.png)
![\includegraphics[height=3in,width=3in]{2nd_all_neg_nullcline}](img343.png)
![\includegraphics[height=3in,width=3in]{2nd_all_neg_init}](img344.png)
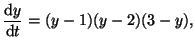
![\includegraphics[height=3in,width=3in]{two_stables}](img346.png)