


Next: Chi-Square Goodness of Fit
Up: How to ask questions
Previous: P-Values
Index
Click for printer friendely version of this HowTo
Estimates of parameters can be based upon different amounts of information.
The number of independent pieces of information that go into the estimate of
a parameter is called the degrees of freedom (df). In general, the degrees of
freedom of an estimate is equal to the number of independent values that go
into the estimate minus the number of parameters estimated as intermediate
steps in the estimation of the parameter itself.
For example, for a
random sample of 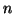 independent data points, if the
sample mean,
independent data points, if the
sample mean, 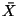 is estimated using the standard formula
is estimated using the standard formula
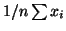 , then
the degrees of freedom for
, then
the degrees of freedom for 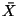 is
is 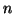 . This is because
. This is because
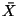 uses
all of the
independent values from the sample and does not rely on any other
parameter estimates in its calculation. However, if the variance,
uses
all of the
independent values from the sample and does not rely on any other
parameter estimates in its calculation. However, if the variance,
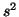 , is estimated using the standard formula
, is estimated using the standard formula
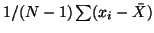 ,
then the
degrees of freedom is equal to the number of independent values (
,
then the
degrees of freedom is equal to the number of independent values (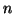 )
minus the
number of parameters estimated as intermediate steps (one,
)
minus the
number of parameters estimated as intermediate steps (one, 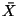 )
and is therefore equal to N-1.
)
and is therefore equal to N-1.



Next: Chi-Square Goodness of Fit
Up: How to ask questions
Previous: P-Values
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19