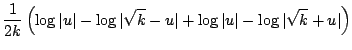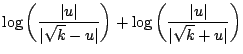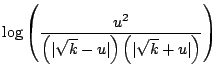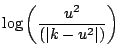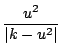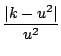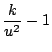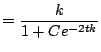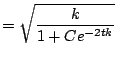|
Solved using the method of seperation of variables and some fancy algebra...
Now, we will break down
First note: and thus, Also note, and Putting together the general concepts in Equations D.2.2, D.2.3, and D.2.4 we get...
So, to solve our non-linear differential equation, we make the substitution...
Next: Vector and Matrix Calculus Up: Derivations For the Curious Previous: Nernst-Planck Equation Index Click for printer friendely version of this HowTo Frank Starmer 2004-05-19 |
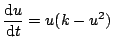
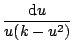
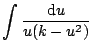
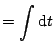
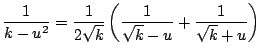
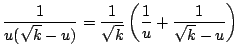
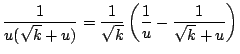
![$\displaystyle \frac{1}{u(k-u^{2})} = \frac{1}{2k}\left[ \left( \frac{1}{u} + \f...
...}{\sqrt{k}-u} \right) + \left(\frac{1}{u} - \frac{1}{\sqrt{k}+u}\right) \right]$](img1119.png)
![$\displaystyle \int \frac{1}{2k}\left[ \left( \frac{1}{u} + \frac{1}{\sqrt{k}-u} \right) + \left(\frac{1}{u} - \frac{1}{\sqrt{k}+u}\right) \right] \textrm{d}u$](img1120.png)
![$\displaystyle \frac{1}{2k} \int \left[ \left( \frac{1}{u} + \frac{1}{\sqrt{k}-u} \right) + \left(\frac{1}{u} - \frac{1}{\sqrt{k}+u}\right) \right] \textrm{d}u$](img1121.png)