or
The Proarrhythmic Potential of Slowed Repolarization and Early Afterdepolarizations (EADs):
Numerical studies of the transition from monotonic repolarization to EADs
C. Frank Starmer June 20, 2004, revised Jan 4, 2005
The mechanism behind spontaneous oscillation in cardiac cells and EADs in particular is sort of fuzzy. While it is well known that reopening of inward channels during repolarization is required to establish a net inward current (and hence initiate a transition from repolarization to depolarization), the details are still fuzzy. I wrote up all this stuff and submitted to Cardiovascular Research last August, 2004. The manuscript was soundly rejected by not 1 but 3 reviewers - all for the same reason - the EAD mechanism is well known.
Realizing that there was a message in the reviewers' comments - I thought about "mechanism" and realized that mechanism means different things to different people. From a qualitative point of view, reopening Ca or Na channels are required for one or more EADs and many investigators are satisfied with this level of detail. But for others, under what circumstances will reopening channels lead to EADs? Channels open and close all the time - under many different conditions. So what is special about repolarization that leads from channel reopenings to EADs. My view of mechanism is from a more physical mechanism perspective - under what conditions will reopening inward channels lead to EADs. My investigations revealed 3 different conditions where the role of reopening could be explored: Reopening during the positive resistance region of the repolarizing i/v curve; Reopening during the negative resistance region of the repolarizing i/v curve; and reopening when the membrane potential is precisely at the transition from the positive to the negative resistance region. While these three conditions are clear to a few (most notably, Otto Hauswirth, Denis Noble and Dick Tsien), there is almost nothing in the literature linking these ideas to EADs. Here I propose measuring the propensity of EADs during repolarization by measuring the development of what I call the EAD safety factor as a function of s1-s2 delay. The safety factor is the current amplitude of the transition from + to - resistance during repolarization. The ideas are demonstrated below.
It all started in 1988 when a patient was admitted to the Duke ER with a ventricular tachyarrhythmia - apparently secondary to an overdose of propolxyphene (use-dependent Na channel blocker). I wondered how such arrhythmias might be triggered. This led to some insights into how use-dependent Na channel blockade increases the duration of the cardiac vulnerable period (1991). This was followed (1995) by studies of spiral waves and how reducing K currents can force a transition from circular spiral tip movement (monomorphic reentry) to meandering (polymorphic reentry) - sort of like TdP. Still I was wondering how reentrant arrhythmias were triggered. Recently, some ideas seemed to spontaneously come together - 10 years being fermented - Most of the numerical experiments use Sergey Missan's CESE system, a java-based numerical electrophysiology experiment environment. I used Grace for the graphs.
Background
Following initial depolarization, cardiac cells either
monotonically repolarize and return to the normal rest
potential or exhibit EADs (plateau oscillations) followed either by
completion of repolarization or incompletely repolarize
and equilibrate at a depolarized equilibrium potential.
Depending on their gating voltage and time dependence, previously inactivated
Na and Ca channels return to the open state and reduce the net
repolarizing current.
As long as the repolarizing current is outward, repolarization continues.
Early studies of Hauswirth, Noble and Tsien [1] revealed that oscillations at plateau potentials were associated with the dynamics of the delayed rectifier and a source of inward current, now recognized to be supplied by reopening Ca channels [2-5]. Moreover they identified the negative resistance region of the repolarizing i/v to be critical in establishing oscillatory activity.
Detailed exploration of the cellular EAD mechanism using in vitro studies has been hindered by the absence of a method to precisely control the time and voltage dependent conductances as they change during repolarization. On the other hand, numerical studies provide the control necessary to dissect many of the complexities of membrane repolarization and demonstrate associations between cellular processes. Such studies have provided important insights linking a number of different modulators of inward and outward currents to EAD production [6,7].
Mutant channels, ion channel blockers, exercise, stress, sleep, drugs that alter transmembrane ion transporters and internal calcium stores, as well as heart rate and pause duration have been associated with conditions associated with sudden cardiac death, supposedly triggered by EADs [8-13]. However, it is still unclear how or whether these observations can be framed in a simple mechanistic characterization of the transition from normal repolarization to oscillatory repolarization. Here I show that the transition from monotonic repolarization to oscillations results from the coincidence of the repolarizing membrane potential and the minimum of the current-voltage relationship at the exact moment the minimum of the negative resistance region = 0. Consequently, proarrhythmia is amplified during repolarization by any increase in availability of inward currents (e.g. delayed inactivation of the fast Na channel) and/or any decrease in the availability of outward repolarizing currents (e.g. loss-of-function in HERG channels). These results also suggest that APD prolongation with a squared repolarization morphology will minimize the time available to develop the negative resistance region and thus be more antiarrhythmic than APD prolongation with triangular-like repolarization.
The Problem and Insights
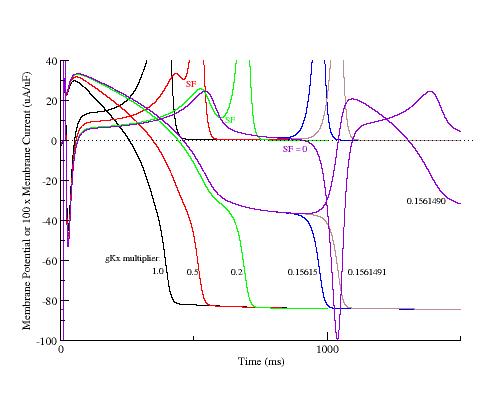
One way to explore EADs is to trigger action potentials with progressively smaller repolarizing currents and observe the relationship between the membrane current and membrane voltage. Shown here are the action potentials and their action currents where the delayed rectifier conductance was progressively reduced, thereby slowing repolarization and increasing the APD. As repolarization slowed, the APD increased and a positive resistance region developed (a result of increasing inward currrents) where reducing Vm reduced the membrane current (indicated by SF) and produced a plateau in the AP. The transition from monotonic repolarization to EADs did not occur until two conditions were met:
- the minimum of the transition from positive resistance to negative resistance region (SF) was 0 uA/uF and
- the membrane reached the potential associated with SF=0 at the same time the SF became zero.
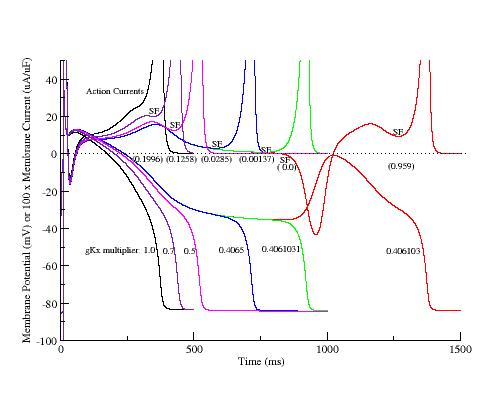
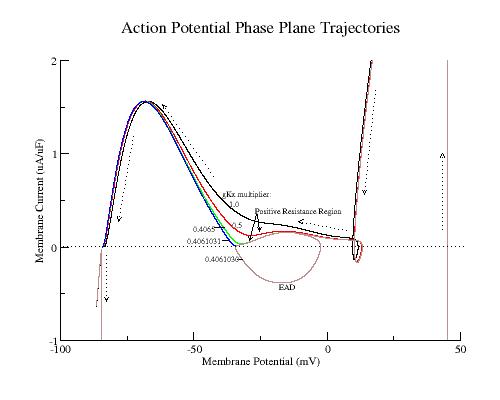
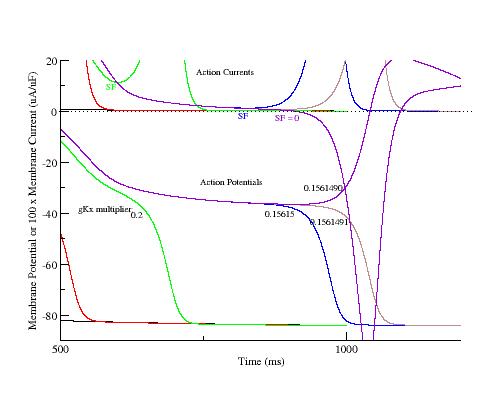
The phase plane portrait illustrates the two competing processes - that of membrane repolarization and that of growth of the negative resistance region. Here is shown phase portraits of a control AP, two intermediate APs (gK multiplier = 0.5, 0.4065), an AP near the transition from monotonic repolarization to EADs (gK multiplier = 0.4061031) and an AP with an EAD (gK multiplier = 0.4061030). Slowing repolarization gradually reduced the minimum of the negative resisitance region (Safety Factor, SF). Note the transition from monotonic repolarization to EAD occured when the phase point (Vm, Im) touched the i=0 axis.
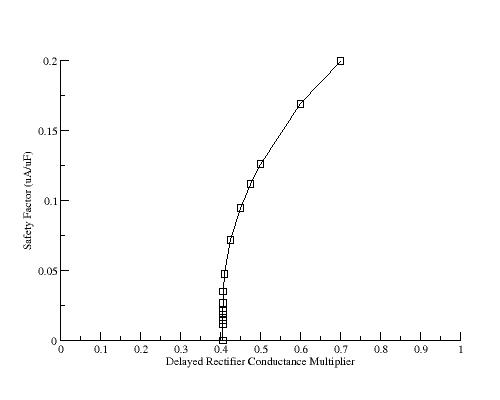
For the LR1 ventricular model, the control action potential shows and outward negative resistance region until a transition back to a positive resistance region at about -60 mV. As repolarization is slowed secondary to reducing gKx, a small outward positive resistance region develops at about -20 mV, passes through a minimum to a negative resistance region and then returns to a positive resistance at about -60 mV. For multipliers > 0.7 there is no negative-positive-negative transition in resistance so that there is no minimum and no SF. Shown below is the value of the minimum (SF) as a function of gKx.
Many cellular processes can modulate the amplitude of inward and outward currents. Specifically a regular rhythm results in accumulated open delayed rectifier channels as well as alterations in the Ca stores. If the SF hypothesis is correct, then SF profiles measured under dynamic conditions using a conditioning pulse train followed by a delay (s1-s2) and a test pulse should display the similar SF reductions secondary to deactivated IK during repolarization as s1-s2 delay increases observed with SF profiles secondary to explicit reduction in gKx measured from APs initiated from equilibrium initial conditions.
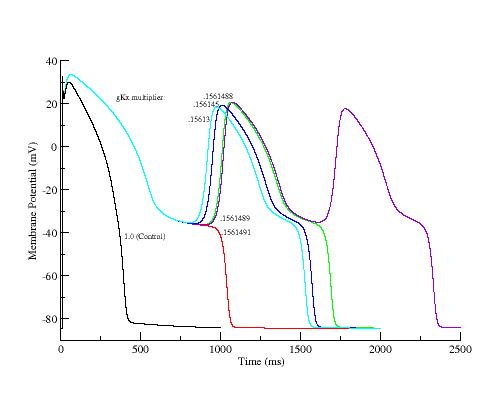
To demonstrate the generic property of the SF mechanism, I have plotted the APs and action currents as a function of s1-s2 delay following 40 conditioning pulses at 2Hz. Note the monotonic reduction in SF as the s1-s2 delay is extended. The earliest AP (black) was with s1-s2 = 500 ms, the same as the conditiong 2Hz train. The EAD occurred when s1-s2 = 1140 ms. Shown also are intermediate are APs and action currents with delays ranging from 1000 ms to 1139.995 ms.
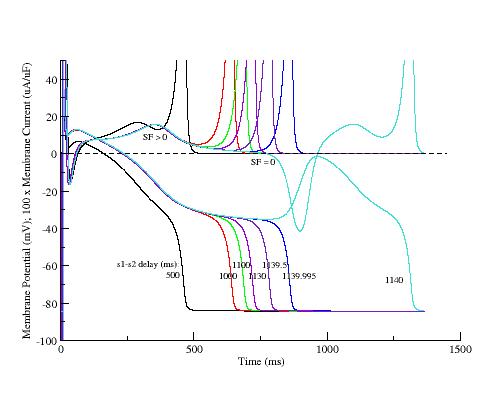
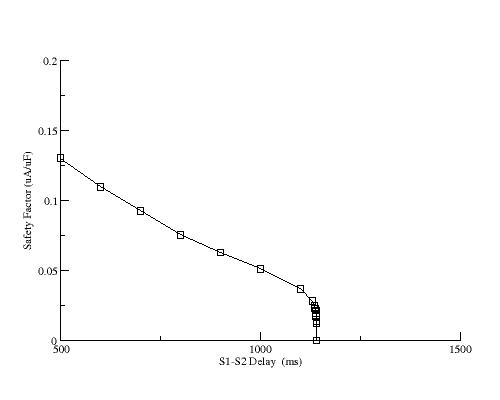
Shown here is the increase of the positive resistance region as a function of s1-s2 delay
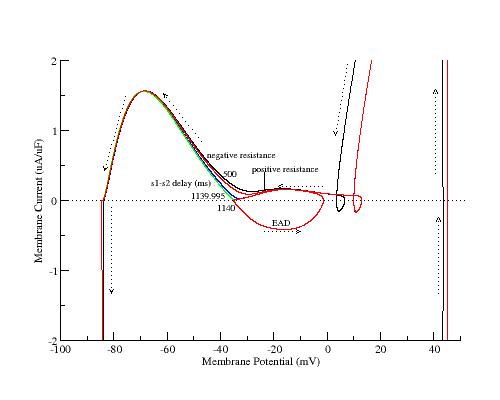
Similar to explicitly reducing gKx, implicit reduction of gKx by
increasing the s1-s2 delay reduces the SF.
A Qualitative Model
These observations demonstrate that repolarization morphology is sensitive to the location of the repolarizing membrane potential, Vm, relative to the negative resistance region of the repolarizing i/v. Specifically, if the membrane potential enters the negative resistance region of the repolarizing i/v before the SF = 0, then repolarization accelerates (phase 3) and terminates after reaching the normal rest potential. If, on the other hand, the membrane potential remains on the positive resistance limb of the repolarizing i/v after the SF = 0, then repolarization is stabilized with the result of plateau arrest. Finally, if the membrane potential reaches the minimum of the negative resistance region at the moment that the SF = 0, then an EAD will result. When Vm reaches the minimum and SF = 0, repolarization is transiently arrested (because the net membrane current is zero) and as the Ca channels continue to recover, the SF becomes negative and Vm gradually shifts from repolarization to depolarization.
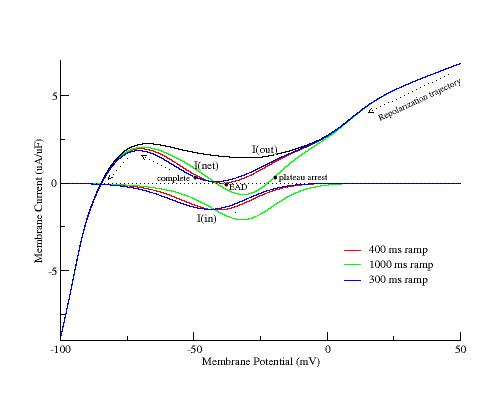
Below are plotted three i/v curves using a reverse ramp from +50 to -100 mV with durations of 300, 400 and 1000 ms. Shown is the total outward current, I(out), the total inward current, I(in), and the net transmembrane current, I(net), = I(in) + I(out). While the total outward current was insensitive to repolarization rate, the total inward current increased as the repolarization rate slowed and the minimum of the negative resistance region shifted to more depolarized potentials. The dots near the minimum of the negative resistance region represent the three possible relationships between Vm and the minimum of the i/v curve. If Vm passes through the mimimum of the i/v and into the negative resistance region before SF = 0 (blue curve), then repolarization continues. If Vm does not reach the minimum of the i/v before the SF = 0 (green curve), then as repolarization continues Ca channels will continue to reopen, shifting the minimum below the i=0 axis and resulting in a stable equilibrium and plateau arrest. However, if the membrane potential arrives at the minimum of the negative resistance region (red curve) at the same time that SF = 0, then an EAD will result. The coincidence temporarily arrests repolarization while Ca channels continue to open, thus initiating a depolarization.
Why does coincidence of Vm and the minimum of the negative resistance region at the moment that SF = 0 lead to an EAD? As shown below, as repolarization is slowed, the peak of the inward current increases and shifts to more depolarized potentials. At the moment that I(Vm) = 0, repolarization is arrested but Ca channels continue to open and increase the total inward current. Thus the instantaneous current at the phase point becomes negative and depolarization is initiated, but at a very slow rate since the total current is very small. As slow depolarization increases, I(Ca) continues to increase thus accelerating the rate of depolarization. Only after Vm reaches the minimum of the I(Ca) current voltage relationship does the rate of repolarization slow and approach the point where I(net) = 0 where the current becomes outward and Vm returns to a repolarizing trajectory as shown in the above phase plot.
EAD sensitivity to altered gating kinetics
Perhaps most interesting is how altered gating kinetics change the window of EAD susceptibility. Mutant HERG channels not only have a reduced conductance but the activation kinetics are slowed. Consequently, based on the above model, we would expect slowed activation kinetics to extend the EAD susceptibility window by further slowing repolarization beyond that associated with reducing gKr. Similarly, increasing the activation rate of Ca channels should amplify the EAD susceptibility range by increasing the rate at which the secondary positive resistance region develops. Below are show the transition (EAD - complete repolarization) conductance multiplier as a function of the activation time constant. Rate multipliers less than 1 reflect slowed activation while multipliers greater than 1 reflect accelerated activation. (By rate multipliers I use multiplier*alpha and multiplier*beta and for the conductance multiplier, I use multiplier * gKx.
Slowing the activation time rate by 0.6 increases the threshold for AP - EAD transition from 0.4061031 to 0.535262 - suggesting that slower kinetics result in EADs with less loss of function (reduced macroscopic conductance)
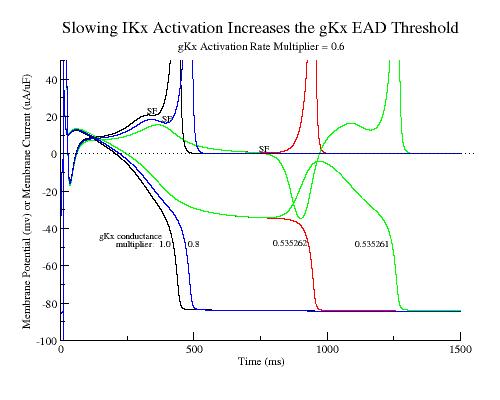
As the IKx activation rate is slowed, the AP-EAD gKx transition conductance dramatically increases. Similarly, as ICa activation is slowed, the AP-EAD gIx transition conductance is diminished
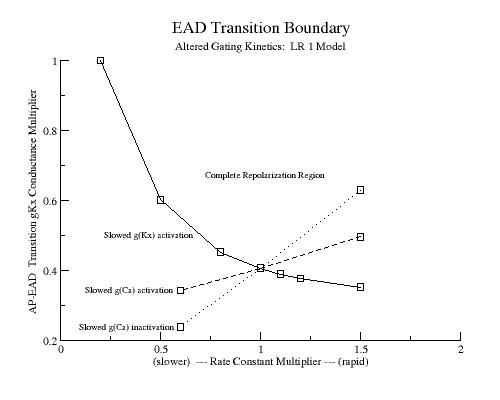
These results suggest that mutations resulting in loss of function by reducing GKr or GKs increase the likelihood of EADs by increasing the likelihood that the phase point of the action potential will find itself within the transition window (above). Further, mutations that increase the time constant of gating changes increase the vulnerability to EADs by increasing the range of GKr or GKs that will place the action potential phase point within the transition region.
Sort of a summary
For EADs, the critical issue is one of the comparative timing of the repolarization potential and the location of the minimum of the transition from positive to negative resistance. If they coincide when the current associated with the minimum is zero, then EADs will occur. I define a safety factor (SF) as the current associated with the minimum of the transition from positive to negative resistance . Now to better understand the influence of timing on EAD production, consider the following three options:
- Vm passes the minimum of the resistance transition region while SF > 0 This condition always results in accelerated repolarization since the membrane potential, Vm, is on the negative resistance limb of the iv when the current is outward.
- The minimum of the resistance transition region passes through i=0 before Vm gets there. The result is either sustained depolarization or a long long wait until intracellular Ca stores force repolarization.
- Vm reaches the minimum of the resistance transition region at exactly the same time as SF = 0. This results in an EAD.
Now complete repolariation is easy. If Vm manages enter the negative resistance region before SF=0, then repolarization is accelerated due to the negative resistance. One could say, but what if Vm was just barely past the minimum, could not continued restoration of gCa pull Vm down and start an EAD? The answer is no - at least from these numerical studies. For this to happen, there would be an increase in repolarization rate (as Vm enters the negative resistance region) before an EAD is triggered. I have never observed this in any numerical studies and think there must also be an mechanistic answer to the question.
Now what about Vm is near the minimum but on the positive resistance side of the i/v. In this case EADs are not possible because if Vm continued to repolarize, but the instantaneous current became negative, then the inward current would drive it back to a depolarized potential where i=0 - a stable equilibrium. In this case, there would be sustained depolarization (at least until the intracellular calcium stores and Na/Ca exchange did their thing while Vm hung around at the sustained depolarization potential and forced continuation of repolarization). This is not seen in either BR or LR1, but is easily seen with LR2 with its more accurate Ca model.
So that leaves Vm arriving at the minimum of the i/v at precisely the same time that the SF = 0. Continued recover of gCa will move the minimum into inward current territory and once Vm crosses over i=0 (in the phase plane), the EAD oscillation is triggered.
There are several predictions based on this model and logic
- higher repolarization rates will be associated with longer delays before EAD takeoff
- higher repolarization rates will be associated with more negative takeoff potentials.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Demonstration of comparable results from BR, LR1 and LRd models
EAD spectra with BR
(EADs were impossible with original parameters so gCa was
set to 1.5 original value in order to force the resistance transition
region to cross i=0 with slowed repolarization)
BR action potentials and associated action currents show a reduction in amplitude (SF) as repolarization is slowed.
BR action potentials and currents with expanded axis reveals the coincidence of Vm with the minimum of the negative resistance region is zero.
EAD spectra with LR 1
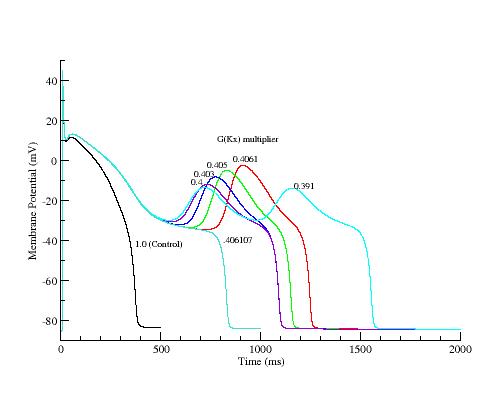
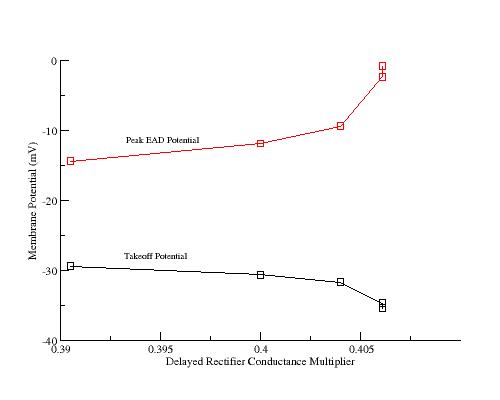
Plot of takeoff potentials and peak potentials for EADs generated by the
LR 1 model.
EAD spectra with LRd (LR 2)
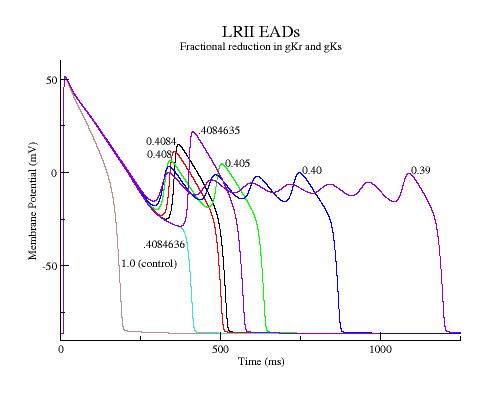
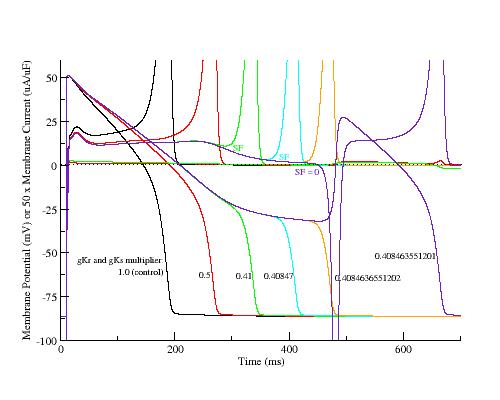
LRd action potentials and associated action currents reveal depolarizing shift in the minimum of the negative resistance region and reduction in amplitude (SF) as depolarization is slowed.
Theoretical considerations
The temporal trajectory of the repolarizing membrane potential (Vm) is
dictated by the instantaneous current-voltage (i/v) which is a mixture
of inward and outward components: C dVm/dt = -(I(in) + I(out)) .
(Note that analysis of EAD mechanisms can be limited to the study of
two generic currents - one inward and one outward. This is a useful
way to explore the role of complexity in cardiac models and whether
additional complexities alter the generic properites of the
2 current model).
Depending on the nature of the
individual i/v components, there may be regions of positive resistance
(where increases in potential result in increases in current) or negative
resistance (where increases in potential result in decreases in current).
As the action potential repolarizes, some outward currents deactivate while
some inward current carriers reactivate. As seen with the above equation,
when inward current dominates, dV/dt > 0 (depolarization)
while when outward currents dominate, dV/dt < 0 (repolarization).
As the membrane potential follows the repolarization trajectory, what is the relationship between the repolarizing potential and the evolving i/v and specifically the growing source of inward current? During repolarization, nothing unusual happens as long as the negative resistance region falls above i=0. When Vm reaches an outward current negative resistance region, repolarization is accelerated. If, during repolarization, part of the nomally outward negative resistance region evolves such that it crosses the i=0 axis and becomes inward, then EADs are possible.
From numerical studies, I have found that the amplitude of the minimum of the negative resistance region of the repolarizing i/v curve (Safety Factory, SF) accurately measures EAD propensity. The SF can be measured under equilibrium conditions established at the rest potential (which is equivalent to a long pause after a pulse train). A SF profile can be measured as a function of delay following a train of conditioning pulses. The impact of altered inward or outward currents on EAD propensity are readily available by considering the potential alteration of the SF profile. Drugs and channel mutations that decrease the amplitude of the SF profile would be considered arrhythmogenic.
References
- Hauswirth, O., Noble, D. and Tsien, R.W. The mechanism of oscillatory activity at low membrane potentials in cardiac Purkinje fibresJ. Physiol. 1969 200:255-265.
- January, C.F., Riddle, J.M. and Salata, J.J. A model of early afterdepolarizations: Induction with the Ca2+ agonist Bay K 8644. Circ. Res. 1988 62:563-571.
- January, C.T. and Riddle, J.M. Early afterdepolarizations: Mechanism of induction and block. A role of L-type Ca2+ current.Circ. Res. 1989; 64:977-990.
- January, C.T., Chau, V. and Makelski, J.C. Triggered activity in the heart: cellular mechanisms of early after- depolarization. Euro. Heart J. 1991 12:(Supplement F), 4-9
- Fulop, L., Banyaz, T., Magyar, J., Szentandrassy, N., Varo, A. and Nanasi, P.P. Reopening of L-type calcium channels in human ventricular myocytes during applied epicardial action potentials. Acta Physiol. Scand. 2004 180:39-47.
- Viswanathan, P. C. and Rudy, Y. Pause induced early afterdepolarizaitons in the long QT syndrome: a simulation study. Cardiov. Res. 1999; 42:530-542.
- Clancy, C.E. and Rudy, Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature 1999; 400:566-569.
- Priori, S.G. and Napolitano,C. Genetics of cardiac arrhythmias and sudden cardiac death Ann. N.Y.Acad. 2004; 1015:96-110.
- Tan, H.L. et al. A sodium-channel mutation causes isolated cardiac conduction disease. Nature 2001; 409:1043-1047.
- Chen, Q. el al. Genetic basis and molecular mechanism for idiopathic ventricular fibrillation. Nature 1998; 392:293-296.
- Mohler, P.J. et al. Ankyrin-B mutation causes type 4 long-QY cardiac arrhythjmia and sudden cardiac death. Nature 2003; 421:634-639.
- Splawski, I. et al. Variant of SCN5A sodium channel implicated in risk of cardiac arrhythmia. Science 2002; 297:1333-1336.
- Chen, Y. et al. KCNQ1 gain-of-function mutation in familial atrial fibrillation. Science 2003; 299:252-254. Choi, G. et al. Spectrum and frequency of cardiac channel defects in swimming-triggered arrhythmia syndromes. Circulation 2004; 110:2119-2124.
- FitzHugh, R. 1961. Impulses and physiologic states in theoretical models of nerve membrane. Biophysical J. 1:445-466.
- Rinzel, J. 1985. Excitation dynamics: insights from simplified membrane models. Federation Proc. 44:2944-2946.
- Hondeghem, L.M., Carlsson, L. and Duker, G. Instability and triangulation of the action potential predict serious proarrhythmia, but action potential duration prolongation is antiarrhythmic. Circulation 2001; 103:2004-2013.
- Roden, D. Drug-induced prolongation of the QT interval. New Eng. J. Med 2004 350 1013-1022.
- Starmer, C.F. Romashko, D.N.,Reddy, R.S., Zilberter,Y.I., Starobin, J.M., Grant, A.O. and Krinsky, V.I. A proarrhythmic response to potassium channel blockade Circulation 1995;92:595-605.

This work is licensed under a Creative Commons License.
C. Frank Starmer