The Story of the Guarded Receptor Model of Use-dependent Ion Channel Blockade

The Challenge: Why channel blockade is different from ordinary (continuously accessible binding sites) binding of ligands to receptors

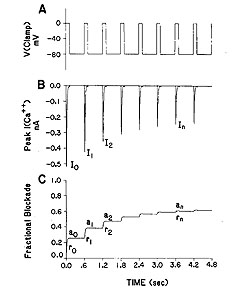
Here is a typical measurement of an inward current in a cardiac cell, in this case, a calcium currrent. The top panel illustrates the voltage clamp potential - alternating between a rest potential of -80 mV and a test potential of 0 mV. With each stimulus, calcium channels open and calcium ions flow into the cell - as shown in panel B. However, in the presence of a channel blocking agent, something interesting happens. With successive pulses, the peak inward current is reduced - as if the more you "use" the channels, the larger the fraction of blocked channels. This is the origin of the term "use-dependent". Panel C illustrates what we think is happening. Instead of the binding site being continuously accessible as with many other receptors (e.g. beta adrenergic, seratonin, alpha adrenergic, ACh ) many ion channel binding sites appear to be sensitive to channel conformation, with periodic activation, it appears that the binding site is only transiently accessible. Stated another way, during the rest phase of stimulation, the receptor binding site is "guarded" and inaccessible. However, during the excitation phase of the stimulation, the receptor binding becomes accessible so that binding is possible. Thus, during excitation, there is an exponential incorporation of drug by channels but during the rest phase, drug is free to escape (with an exponential time course) from the binding site (untrapped) or cannot escape (trapped). Because this process differs from the type of binding seen in typical ligand-receptor systems (e.g. beta receptors), it has been unsuitable to traditional analysis, i.e. using equilibrium dose-response curves to estimate the Kd.

Why is modeling channel blockade interesting? There is considerable clinical evidence that a large class of antiarrhythmics are proarrhythmic. In addition drug overdose victims often appear with ventricular tachyarrhythmias - and many abused substances are use-dependent Na channel blockers. Some recent progress with understanding the proarrhythmic properties - as it relates to the cardiac vulnerable period is available by clicking here . There is also a new (2001) manuscript describing how antiarrhythmic drugs can increase the rate of sudden cardiac death This paper is basically a physics paper - taking the mechanisms behind wave formation and ion channel blockade and demonstrating how slowly unbinding Na channel blockers can increase the region of vulnerablility in cardiac tissue.

Below is our story - starting with ideas posposed by Bertil Hille and ending with a detailed analysis based on our model of periodically accessible binding sites (the Guarded Receptor Hypothesis). (Note added August 16, 2000: After some detailed analytical and numerical studies of Hille's modulated receptor model and the recent Allosteric model of Jeff Balser, it seems quite useful to consider all the models of ion channel blockade as either cyclic (Modulated and Allosteric models) or acyclic (Guarded Receptor model, Clay Armstrong's model of TEA block ). Cyclic models represent a cycle of steps that return to some "initial" step whereas, for acyclic models, one cannot return to the "initial" step without retracing the steps that took you to the blocked state. The utility of the linear or acyclic models is that they readily admit to analytical solutions and robust parameter estimation procedures. Often, when cyclic models have one low flux component, they can be considered equivalent to the behavior of acyclic models where analysis tools are readily available: Starmer, CF and Grant, AO: Phasic ion channel blockade: A kinetic model and method for parameter estimation. Molecular Pharmacology 28:348-356, 1985; Starmer, CF, Packer, DL and Grant, AO: Ligand binding to transiently accessible sites: Mechanisms for varying apparent binding rates. J. Theor. Biol. 124:335-341, 1987, Starmer, CF. Characterizing activity-dependent processes with a piecewise exponential model. Biometrics, 44:549-559, 1988 )

Look at this for ideas and insights into the proarrhythmic potential of antiarrhythmic drugs .

In the beginning ...

It all started in Joe Greenfields office in late 1980. Joe had just become chief of cardiology (at Duke) and was in the process of interviewing everyone in the division. During my interview, Joe correctly noted that I was not having "fun" with the Cardiology Database that Bob Rosati and I had started 12 years earlier - and that perhaps I might help Gus Grant and Harold Strauss with some cardiac pharmacology problems. In Joe's words, Harold was threatening to go to NC State to study math- which would be a disaster - so why couldn't I join up and see what I could do to help.

A quick meeting with Gus and Harold revealed that what they really wanted was a programmer to code the Hille Modulated Receptor model so that they could estimate rate constants. Being an engineer of very little brain, I looked at the paper and could not understand it (either the Hille original model nor the Hondeghem-Katzung variant). The problem was that the model as described by Hondeghem and Katzung seemed over-determined - like fitting a unique straight line through a single point. This was because Hondeghem proposed a shift in the "h" curve for inactivation of drug-complexed channels, and such a shift cannot be "identified" because it cannot be separated from a shift caused by voltage dependent blocking. Thus the MRH was initially not very interesting. Because of the ambiguity introduced in the MRH with shifted inactivation in drug-complexed channels, I made a counter proposal: lets simply use ordinary ligand-receptor binding kinetics applied to a linear reaction sequence (in contrast to a loop or cyclic reaction sequence) and see how many observations we can account for. It turned out that by ignoring the altered gating in drug-complexed channels, it was possible to account for, with quantitative accuracy, use-dependent profiles, frequency-dependent profiles as well as shifted channel availability curves for all data that I was able to get my hands on (both published and unpublished). Thus, the birth of the guarded receptor model - which in reality was an extension of Clay Armstrong's linear model of TEA block of K channels. Our contribution was to derive equations that permitted almost trivial estimation of the rate constants. Further, Jay Yeh agreed to test the model and estimation procedure with QX222 during one of his Wood's Hole summers - and then Stan Nattel's group verified it and of course, a number of fellows in our lab (Rosey Gilliam, Doug Packer, David Wendt, Mike Barber, Yuri Zilberter, et al) also verified it.

Here, I'll bring together the story of the guarded receptor model and demonstrate how it facilitated identification of the proarrhythmic effect of all Na channel blockers.

The Modulated Receptor Paradigm: A Cyclic Blockade Process

Bertil Hille and his graduate students, primarily Gary Strichartz and Ken Courtney developed an elegant model to provide an explanation for use- and frequency-dependent ion channel blockade. The interesting feature of blockade of many ion channels is that the fraction of drug-complexed channels depends on the frequency of stimulation. Thus there is some suggestion that the binding site is not continuously accessible as with traditional ligand-receptor binding models - e.g. antagonist binding to beta receptors. After Ken presented the Seattle groups ideas at UCSF, Luc Hondeghem and Bert Katzung immediately developed a variant for cardiac cells and began to explore the properties of antiarrhythmic drugs.

The model is as shown here - with binding to each of the three dominant channel conformation: rest, activated and inactivated. The model is rather complex from a parameter estimation point of view in that there are 6 rate constants for drug-channel interactions as well as 4 channel transition rates for drug-complexed channels - 10 parameters must be estimated for application to a drug that blocks all three conformations.

Modulated Receptor Model as expressed by Hondeghem and Katzung and Hille's Simplified Blocking Model (Used below by me to show Use-dep block

This conservation of mass equation illustrates how the rate constants for I* <===> R* must be adjusted to maintain conservation of mass. Note that the ratio of forward to reverse rate constants must be maintained - which means that the rate constants can be scaled by a common factor - thereby preserving the equilibrium dissociation property but altering the time-constant for eaching equilibrium. What I did not understand earlier, was that the primary requirement for use-dependent blockade in a loop model was that the altered rate constants must be altered in a manner that creates a major difference (at this moment, I don't know how much difference) in the time constants : 1/[a(h) + b(h)] for R <==> I and R* <==> I*

Looking at this with a little more detail, at equilibrium b(h)R = a(h)I. So I = b(h)/a(h) R. Similarly, k(I)[D]I = l(I)I* . Hille defines the equilibrium dissociation constant (see above) as including the concentration, i.e. Ki = l/k[D] where l is the unbinding rate and k is the binding rate so we can write I* = I/Ki. Continuing around the loop, R* = a(h*)/b(h*) I* and finally, R = Kr R*. Writing the conservation of mass: R = b(h)/a(h) * 1/Ki * a(h*)/b(h*) * Kr * R. Consequently b(h)*a(h*)*Kr = a(h)*Ki*b(h*). What is the challenge of this approach? Its that an exact modification of a numerator rate must be precisely balanced by a change in a denominator rate. This has been referred to as an allosteric effect by Jeff Balser.

I initially thought that such a model could not produce use-dependent blockade, since once equilibrium is achieved, channels simply shuttle back an forth between drug-free states or drug-complexed states - but not between drug-free and drug-complexed states (because the driving force of the drug-binding reaction is always in equilibrium. Hille suggested that this could be satisfied by requiring modified inactivation kinetics.

Hondeghem/Katzung then proposed that there was simply a voltage shift in the gating kinetics, thus preserving the mass balance. This is incorrect, because a simple shift in the rates does not preserve the ratio of the rates, as required by a detailed balance. Moreover, such a shift cannot be measured experimentally (at least with electrophysiologic measurements) because blocked channels do not conduct and thus inactivation of drug-blocked channels cannot be detected.

Recently, though, I was challenged by Jeff about loop reactions and the possibility of displaying use-dependent blockade. After some additional thought it occurred to me that if the time constant of transitions between rest and inactive states was significantly different from the time constant of transitions between drug-complexed states, then use-dependent block would be possible. So, I made a simple 4 state model and assumed block of rest channels to have a Kd approximately 100x larger than that of block of inactivated channels.

R <==> I <==> I* <==> R* <==> R

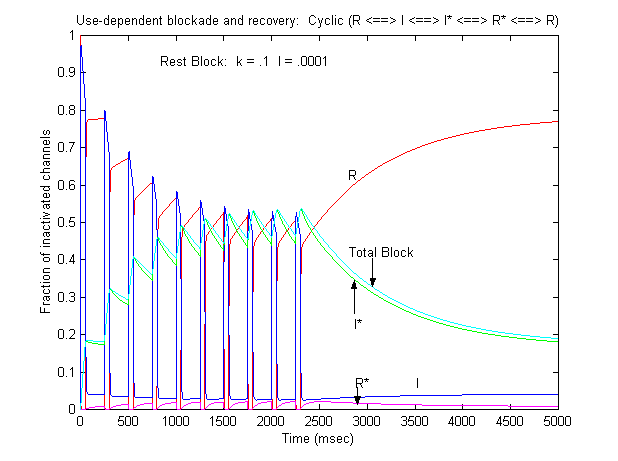
The result was use-dependent block as seen here where

red = rest channels

blue = inactivated channels

green = blocked inactivated channels

magenta = blocked rest channels :

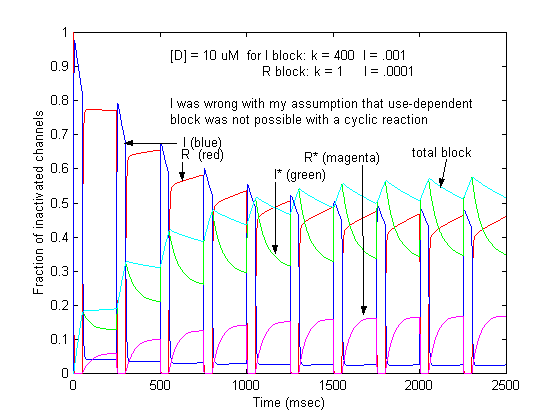
Some interesting observations: Pulse train stimulation with a 50 ms depolarizing pulse (-20 mV) and 200 ms recovery at -80 mV. The green trace is the fraction of blocked inactivated channels (I*). Note that at the beginning of each stimulus pulse (at 0, 250, 500, 750 etc) there is a jump in I* which reflects that rapid transition from R* to I*. This is followed by an exponential block for the 50 ms clamp interval. And then there is a 200 ms interval of slow recovery. During "recovery" there is an exponential increase in R* (shuttled from I*) which represents the slower time constant of state transitions for drug-complexed channels. Blue is the fraction of unblocked channels in the rest state and red, the fraction of inactivated channels. Lots of interesting speculation with this figure. To my knowledge, its the first demonstration of use-dependent block using a loop model that satisfies conservation of mass (detailed microscopic balance).

A matlab script for the removal of the matrix singularity and solution of the system of ode's is here. A matlab script for the rate constants using the BR inactivation model and returns the matrix of coefficients for a 4 element loop is here

If one looks carefully at the blocking pattern at the time the membrane potential is switched, its possible to see that under some conditions, blockade continues to increase. Here is a figure that show use-dependent block from a cyclic process (10 pulses of 50 msec duration, 200 msec recovery interval; Vrest = -80 mV, Vtest = -20 mV) followed by a long recovery interval at -80 mv.

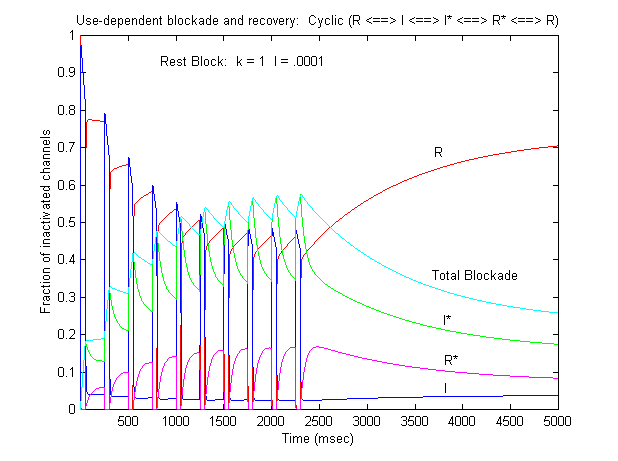
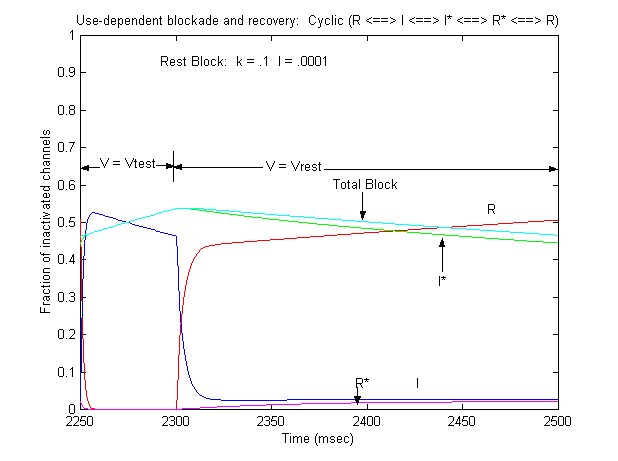
Note that there is an increase in block of rest channels that occurs immediately after the switch to -80 mV. Looking at a single pulse

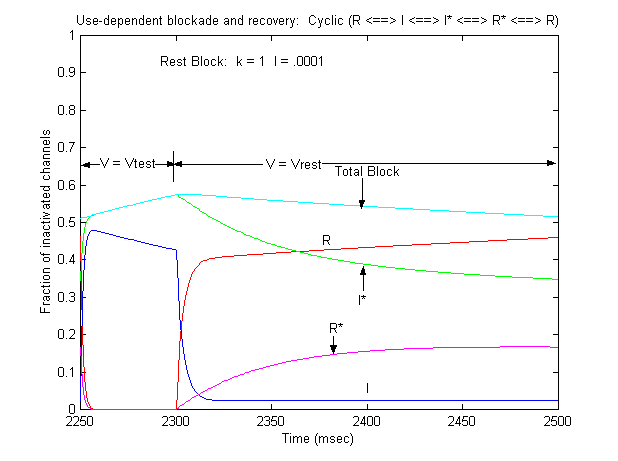
Note that for 10 - 20 ms after the switch in potential from Vtest to Vrest, there is a slight increase in total blockade, (cyan line) that is due to the block of rest channels that is fed by the transition of previously inactivated channels (I) back to the reset state. Because the transition from I* to R* is slow compared with I to R, the R* state is empty immediately after the switch to -80 mV - whereas R is rapidly repopulated. Mass action then produces block of these channels, temporarily increasing total block until the R <==> R* reaction reaches equilibrium. As the binding affinity of the R - R* reaction decreases, so does the transient increase in total block at the test-rest voltage transition as shown here. The rest state binding rate is 0.1/M/msec - whereas above, it was 1/M/msec

Note that the total block closely parallels I*, due to the low affinity of drug for R channels. This is more clearly seen in the expanded figure below

Its clear from the above, that as the binding affinity for rest channels is reduced, one can consider the "loop" reaction as a "linear" reaction, which is the foundation of the guarded receptor paradigm.

This alternative approach is simpler and leads to a quantitatively accurate estimation procedure that produces unique parameter estimates. Lets assume that there is no "rest" block - thus the loop is broken and the blocking process is linear - and that all binding occurs with the inactivated channels where access to the binding site is determined by the channel conformation. Under these conditions, there is no loop and so there is no mass balance reqirement. But much more important, we can test the following hypothesis: can we account for the shift in channel availability seen in the presence of inactivated channel blockers simply on the basis of guarded access? The analysis below demonstrates both theoretically and the theory has been verified experimentally that the observed shift can be completely accounted for by guarded access. Because the guarded receptor model has fewer parameters, and (as shown below) leads to a unique parameter estimation procedure, it would seem to be the model of choice.

Recently, Jeff Balser and his colleagues at Vanderbilt and Johns Hopkins articulated a model of ion channel blockade, which they called an allosteric model ( Kambouris NG, Nuss HB, Johns DC, Marban E, Tomaselli GF, Balser JR. A revised view of cardiac sodium channel "blockade" in the long-QT syndrome, J Clin Invest. 2000 Apr;105(8):1133-40). While the verbal articulation differs from that of the modulated receptor model, it is qualitatively similar, and indeed, suffers from the same problems of parameter estimation and viability with respect to the microscopic balance. To date (7.1.2000), these investigators have not reported demonstrations of use-dependence using their allosteric model. I thought that the above analysis made use- and frequency- dependence of ion channel blockade as described by their allosteric model impossible. I was wrong!!! I thought that with pulse train stimulation, use-dependent block would occur until an equilibrium was reached. At that point, no further use-dependence can be demonstrated because the transition processes for both the drug-complexed and drug-free channels are in equilibrium. The failure of this analysis was my assumption that the time constants of state transitions between drug-free and drug-complexed channels would be comparable. By making the state transitions between drug-complexed channels slow, use-dependence is always possible (discovered on the beach at Kolumvari, Crete - late one afternoon when the water was unsuitable for snorkeling).

The Guarded Receptor Alternative: An Acyclic (linear) Process

My first impression with the Hille model and the Hondeghem-Katzung extension was - well thats nice. The physics is correct, the chemistry looks reasonable - but something does not quite fit. The basis of the uncertainty is shown here: Control (drug free) availability and channel availability in the presence of drug - is this the result of simple voltage dependence of blockade or a combination of events including voltage dependent blockade and modified inactivation kinetics in drug-complexed channels?

Hille's Availability Curves

My concern was that the detailed balance, as shown above, mandated exact changes in the gating kinetics, but how could a simple theoretical construct dictate structural changes to the drug-channel complex?? Moreover, how could such a model be validated? The only possibility of validating it was with gating charge studies - but these are extremely difficult to implement and more difficult to quantitatively interpret.

So, when looking at the availability curves above, it occured to me that there was an alternative that could escape the requirements of a detailed balance. To escape a detailed balance, there must be no loop, so I assumed that there was no blockade of rest channels. With this assumption, what if we simply considered the gating apparatus as limiting drugg access to a binding site? Thus, the shift in availability, as shown above is not the result of modified gating in drug-complexed channels, but rather normal channel availability with an additive loss of availability due to channel blockade. One way to test such an hypothesis would be to predict the shift in the midpoint based on a gate-controlled access model: the guarded receptor paradigm:

Rest <-----> Inactivated <----> Blocked To jump to the end, for a controlled access model, the shift in availability midpoint is determined by

delta V = s ln ( 1 + k[D]/l)

where s is the slope of the Boltzmann function: Avail = 1/(1 + exp(V-Vh)/s) and k and l are the rates of binding and unbinding from the channel substrate, and [D] is the drug concentration.

How did we arrive at the above equation? Assume that the Boltzman function, shown above characterizes normal channel inactivation. In the presence of drug, this equation can be rewritten, based on the above R <==> I <==> B model as

Avail = 1/(1 + (1 + kD/l)*exp(V - Vh)/s)

By rewriting 1+kD/l as exp(ln(1 + kD/l)), we have

Avail = 1 / (1 + exp(V - Vh + s*ln(1 + kD/l))/s)

This equation can then be fit to availability curves measured in the presence of drug and used to make least squares estimates of the binding affinity since the voltage shift depends on both the binding affinity as well as the drug concentration.

Interesting experimental protocols are suggested by these equations. By measuring the time course of incorporation of drug into a channel, one can estimate k and l, then using the above equation, one can predict the shift in availability. Such a test would severely test the guarded receptor paradigm since rate constants from one protocol would be used to predict availability shifts based on the same model. If different processes were operating, the results would not agree. With studies of lidocaine, the agreement between observed and predicted shift was within 5% (See Rosie Gilliam's paper).

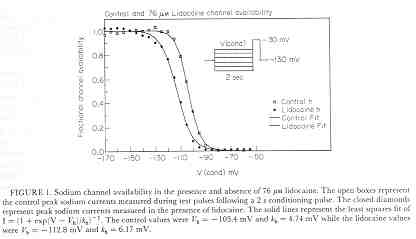
Licodaine Drug-free and 76 uM lidocaine availability

The solid lines represent the least squares fit of

Availability = 1/(1 + exp(V - Vh)/s)

For drug-free conditions, Vh = -103.4 mV and s = 4.74, while for 76 uM lidocaine, Vh = -112.8 mV and s = 6.17. For 15 experiments, the control Vh = -102.4 mV and s = 6.27 while for 76 uM lidocaine, Vh = -112.8 mV and kh = 6.17. Using the shift equation above, a 12 .4 mV shift corresponds to an equilibrium dissociation constant, Kd = 13.1 uM. We also estimated the rates of binding and unbinding from the results of pulse-train stimulation at frequencies. Analysis of the data revealed an open-channel binding rate of 1.36 x 10**6 /M/s and unbinding rate of 39.6 /s. Binding to inactivated channels was characterized by a binding rate of 3.59 x 10**4 /M/s and an unbinding rate of .666/sec. The Kd (l/k) for inactivated channel binding is .666/3.59 * 10**4 = 18.5 uM, in good agreement with the Kd estimated from the midpoint shift in availability curves.

Evidence Against the Modulated Receptor Paradigm

The demonstration that the midpoint shift in availability can be accounted for by simple block of inactivated channels, WITHOUT requiring altered gating kinetics for drug-complexed channels is perhaps the strongest statement against the modulated receptor model. As far as I know, this is the only demonstration that clearly distinguishes the behavior of the Modulated Receptor paradigm from the Guarded Receptor paradigm. As pointed out above, though, the MRH parameters cannot be uniquely estimated - so that it is perhaps useful to conceptualize a process, but quantative studies are simply not possible.

The Guarded Receptor Model

The basic idea behind the Guarded Receptor Model is that access to a channel binding site is controlled by the channel conformation. Schematically we can write:

 

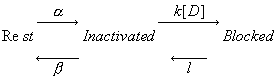
If the gating transition rates are rapid compared with rates of blocking and unblocking then rapid equilibration can be assumed. Under these conditions, let h represent the fraction of non-inactivated channels, h = b/(a+b), then the above reaction can be represented by

 

 

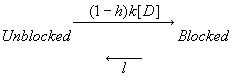
Several critical observations can be made at this point:

1)      Use-dependent and Frequency-dependent blockade requires an asymmetry of rate constants that shift the equilibrium toward and away from the Blocked state with changes in the membrane potential. Without this asymmetry, an equilibrium would be achieved after some time that would not vary with additional changes in transmembrane potential.

2)      Blocking channels will increase shift more rest channels into the Inactivated state due to simple mass action. Consequently, at the rest potential where h is near 1, there can be significant tonic block, simply due to block of channels that are inactivated at the rest potential.

 

A early test of the guarded receptor paradigm consisted of simply testing the above simplified model by estimating the equilibrium dissociation constant with two different stimulation protocols, the inactivation protocol and a pulse-trains applied at different stimulation frequencies.

 

In order to grasp the underlying simplicity of the above approach, I derive the main relationships for blockade of a periodically accessible (guarded) binding site. I start by reviewing binding to a continuously accessible site and then extending it to a periodically accessible binding site.

 

Contnuously accessible sites exhibit exponential binding are the process is described by

 

where 1-h is the fraction of channels with accessible binding sites and k and l are the rates of binding and unbinding respectively. The solution to this differential equation is exponential, as shown in the above figure. We show here, two stages of binding: 1) associated with the activation of the channel for 250 ms and 2) when the channel returns to the rest state. Here, the red curve depicts binding when all channels have accessible binding sites (activated state) while the green curve depicts binding (in this case, net unbinding) when no channels are accessible (h = 1).

 

We now explore pulse train stimulation. Assume a train of pulses that switch the membrane potential between a rest value, V_r and an activated value, V_a. Let an represent the fraction of blocked channels at the end of the nth activated pulse be a_n and the fraction of blocked channels at the end of the nth recovery pulse (return to the rest potential), r_n. Let k_a, l_a, k_r, l_r be the apparent rates of blocking and unblocking – i.e. for inactivated channel block where the guard function is (1-h) then k_a = k(1-h).  Then if the activated interval is t_a and the recovery interval is t_r, we can write

 

 

 

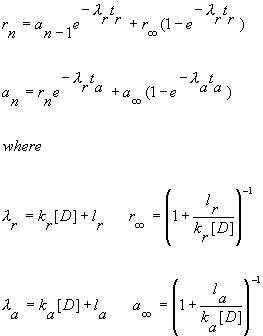
Combining the equations for r_n and a_n, we can write:

 

 

 

These equations can be readily solved (once you’ve done it the first time – somewhere along the way in engineering school, solving discrete recurrence equations escaped the curriculum), leading to solutions that are the periodic equivalent to the continuous binding process:

 

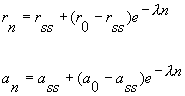
where

 

 

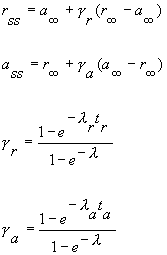
From this, its obvious that the membrane current just prior to stimulus transitions of a periodic piecewise exponential process follow an exponential sequence with a rate that is the linear function of the state-dependent rates and a steady-state that is a linear function of the state-dependent equilibria. These results, in fact, suggest experimental protocols for testing this model e.g. pulse train stimulation at different frequencies should yield a linear relationship between l and t_r and another linear relationship between steady-state block and g. Rosey Gilliam verified this with studies of lidocaine block of cardiac sodium channels and Jay Yeh verified it with studies of QX222 block of squid Na channels. Here is a typical set of lidocaine blockade data demonstrating the frequency dependent effect: the higher the frequency of stimulation, the greater the blockade (from Rosey Gilliam's work).

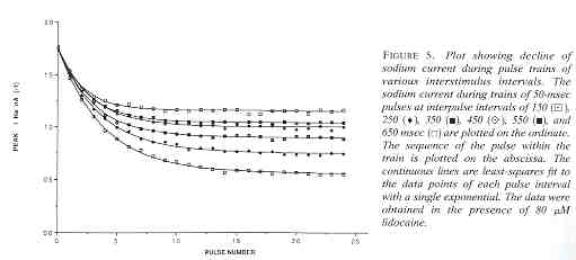
Below is a sample of Jey Yeh's data from squid giant axon. QX222 was used, a permanently charged lidocaine analog with stimulation rates ranging from 10 Hz to .1 Hz. The pulse constant is the exponential rate obtained from a least squares fit of the uptake curve for a particular frequency (see above uptake curves from Rosey's data). Each curve is fit using least squares fit of r(n) = r_ss + (r₀ - r_ss)e^-ln where n is the pulse number. Below is a plot of l vs stimulus interval (left plot) and steady-state block (r_ss) vs g (see above derivation) :

 

 

 

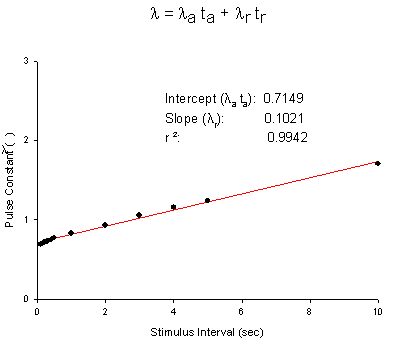
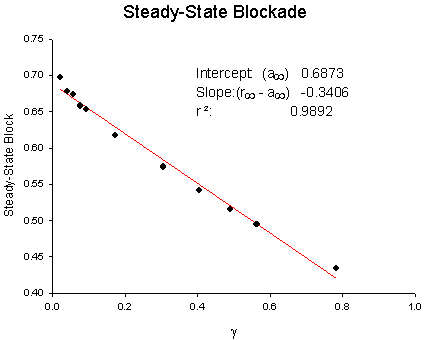
From these plots, the apparent rates of binding and unbinding can be estimated: l_a = k_a[D] + l_a, l_r = k_r[D] + l_r; a(inf) = k_a[D]/( k_a[D] + l_a) , r(inf) = k_r[D]/( k_r[D] + l_r). For this example, we can assume a mean open time of 1 ms (t_a) so that l_a = 714.9/s and lr = .102/s . k_a[D] = a(inf) * l_a = .6873 * 714.9 = 491.3. Assuming [D] = 2 mM, then k = 2.45 x 10⁵ /M/s and l = l_a - k_a[D] = 714.9 - 491.3 = 223.6 /s .

 

Modeling Ion Channel Blockade in a Membrane Model

 

 

Above we demonstrated how to collapse a microscopic (i.e. channel-conformation dependent) model of ion channel blockade into a generic reaction between drug and unblocked channels:

For example, block of channels making the transition from the rest to the inactivated conformation can be described exactly as :

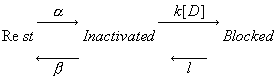
Let h = fraction of non-inactivated channels: b/(a+b). Then we can approximate this kinetic scheme, using the assumption that channel conformation transitions rapidly equilibrate relative to drug binding as:

 

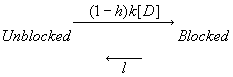
The differential equation describing this is simple which can be written in a more generic form for the following model:

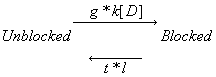
where g is a general "guard" function that describes the fraction of accessible channels and t is a general "trap" function that describes the fraction of blocked channels where the drug is trapped and cannot escape. This scheme is readily described by . In the case of block of inactivated channels, g = (1-h); for open channel block, g = m³h, assuming the Hodgkin-Huxley channel formalism.

 

To incorporate the drug model into a standard description of an excitable membrane (HH, Lou-Rudy, Beeler-Reuter), its only necessary to add the blockade differential equation and modify the conductance of the channel being blocked. For the standard HH Na model, we write gNa = gbarNa*m³h(1-b) where gbarNa is the maximum Na conductance.

 

Look at results of exploring the cardiac vulnerable period at /sample.html for results from studies exploring the basic nature of propagation in an excitable medium and at : /vp.html for insights into drug effects on cardiac conduction and cardiac arrhythmias.