C. Frank Starmer September 4, 2007
Duke-NUS Graduate Medical School Singapore

Spiral wave initiation: A conditioning wave followed by
excitation within the vulnerable region
 Rushton realized that in order to trigger sustained propagation, a
critical region of tissue must be excited (referred to as the liminal
length, Rushton, W.A.H. 1937. Initiation of the propagated disturbance.
Proc. R. Soc. Lond. (Biol.) 124:210-243). The mechanism is a
threshold - the initial disturbance must be able to raise adjoining
regions above their threshold via a diffusive process.
Later Neu and colleagues
linked this concept with an approximation of the critical nucleus
(Neu, J.C., Preissig, S.R. and Krassowska, W. Initiation of propagation in a one-dimensional excitable medium. Physica D 102: 285-299, 1997.).
Bountis and colleagues (
Bountis, T., Bezerianos, T. and Starmer, C.F. Wave front formation in
an excitable medium by perturbation of solitary pulse solutions. in
Proceedings of the 4th School "Lets Face Chaos through Nonlinear
Dynamics" Maribor, Slovenia, 1999, Ed. by M. Robnik. Prog. Theor.
Phys. Suppl. 139: 12-33, 2000.) realized that that the
stationary wave could be used to explore stimulation parameters that
either decayed or expanded. They derived
an analytic expression for the standing wave
in terms of the Fitzhugh-Nagumo model parameters.
Rushton realized that in order to trigger sustained propagation, a
critical region of tissue must be excited (referred to as the liminal
length, Rushton, W.A.H. 1937. Initiation of the propagated disturbance.
Proc. R. Soc. Lond. (Biol.) 124:210-243). The mechanism is a
threshold - the initial disturbance must be able to raise adjoining
regions above their threshold via a diffusive process.
Later Neu and colleagues
linked this concept with an approximation of the critical nucleus
(Neu, J.C., Preissig, S.R. and Krassowska, W. Initiation of propagation in a one-dimensional excitable medium. Physica D 102: 285-299, 1997.).
Bountis and colleagues (
Bountis, T., Bezerianos, T. and Starmer, C.F. Wave front formation in
an excitable medium by perturbation of solitary pulse solutions. in
Proceedings of the 4th School "Lets Face Chaos through Nonlinear
Dynamics" Maribor, Slovenia, 1999, Ed. by M. Robnik. Prog. Theor.
Phys. Suppl. 139: 12-33, 2000.) realized that that the
stationary wave could be used to explore stimulation parameters that
either decayed or expanded. They derived
an analytic expression for the standing wave
in terms of the Fitzhugh-Nagumo model parameters.
A primary insight is that the configuration of a stationary wave is a function of medium excitability - not surprising, but important. Shown to the right are standing wave profiles as a function of excitability using the Fitzhugh-Nagumo model where the slow (inhibitory) current is constant: W(x,t) = constant. As illustrated, the standing wave for the most excitable medium (W = -0.3, black curve) is smaller than the least excitable medium (W = -0.1, magenta curve).
I will use these concepts to illustrate vulnerability, the state of non-uniform excitability where excitation produces an asymmetric respone where propagation succeeds in some directions and fails in other directions (unidirectional conduction). For initiating sustained propagation, a disturbance must excite a region exceeding that of the stationary wave. As the excitability is reduced the size of the critical nucleus increases as shown here.
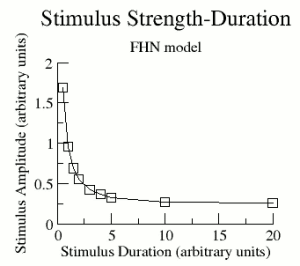 Shown here is the relationship between the stimulus amplitude and the stimulus
duration required to excite a region producing a standing wave.
For a fixed pulse duration, the amplitude was varied to identify the transition
between successful and unsuccessful propagation. The observed
amplitude of the stimulus pulse varied inversely with the duration of
the pulse. Conceptually, the relationship can be visualized in terms
of charge transfer from the stimulus electrode and adjacent tissue.
Consequently short pulses require a larger amplitude for
transferring the required charge than long duration pulses as shown here.
Shown here is the relationship between the stimulus amplitude and the stimulus
duration required to excite a region producing a standing wave.
For a fixed pulse duration, the amplitude was varied to identify the transition
between successful and unsuccessful propagation. The observed
amplitude of the stimulus pulse varied inversely with the duration of
the pulse. Conceptually, the relationship can be visualized in terms
of charge transfer from the stimulus electrode and adjacent tissue.
Consequently short pulses require a larger amplitude for
transferring the required charge than long duration pulses as shown here.
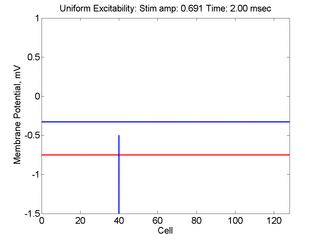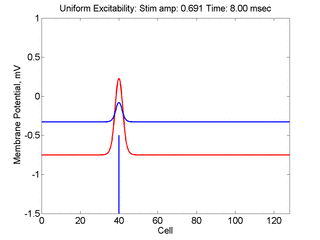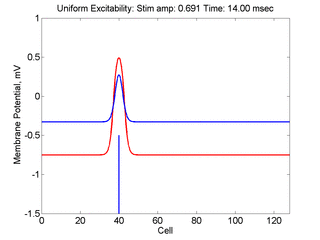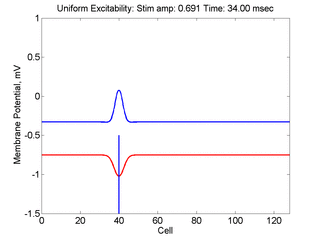
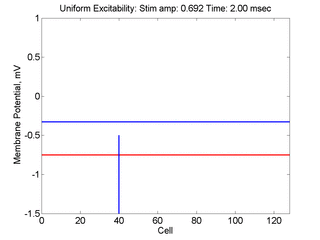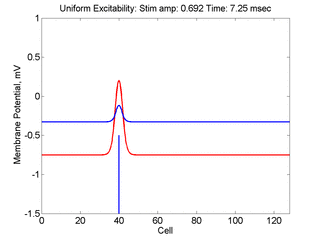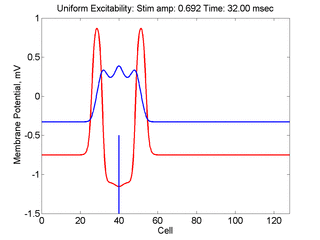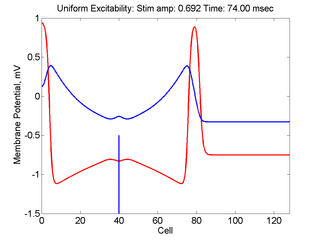
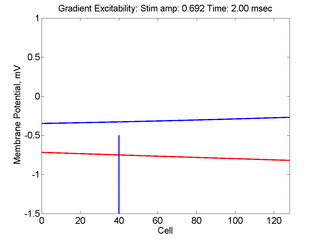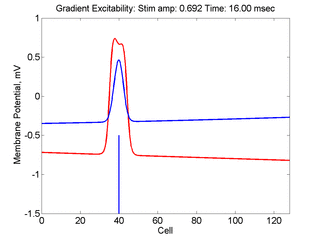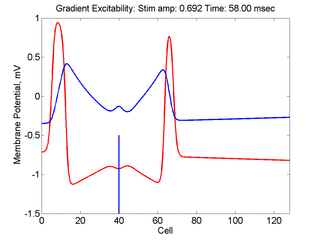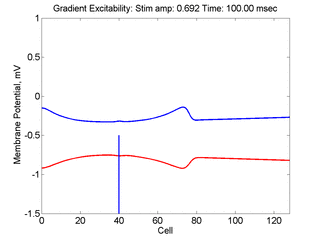
Vulnerability is the asymmetric response to disturbing an excitable medium. By asymmetric, I refer to initiating a propagating wave in some directions while propagation fails in other directions. Shown below are responses to near threshold stimulation as determined from the strength-duration curve above. For subthreshold excitation, we used 0.691 for 1.5 time units while for suprathreshold excitation, we used 0.692 for 1.5 time units.
- Left Panel: When the excitation is subthreshold (0.691), the initial impulse expands to that of the stationary wave and hesitates (at about 5 time units) and then continues to expand. As the inhibitory current continues to grow, the front initiates a collapsing phase.
- Right Panel: When the excitation is suprathreshol (0.692), the initial disturbance again expands to that of the stationary wave, hesitates and then continues to expand, eventually splitting into two fronts propagating away from the stimulation site.
- Lower Panel: Here, the medium exhibits a linear gradient of
excitability while the fast function is unmodified as described here:
- epsilon * dU/dt = U*(1 - U*U) - W + Istim. The stimulus width was 21 units, its duration = 1.5 time units.
- dW/dt = gamma*U + beta + grad*x where beta (3.8) and gamma (5.5) are model parameters, epsilon is the time scale factor (.01) and grad = 0.005.
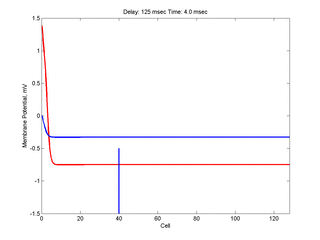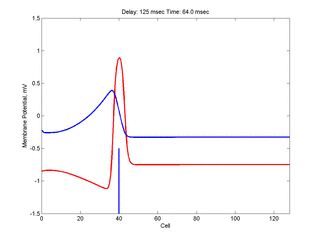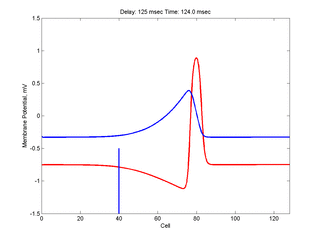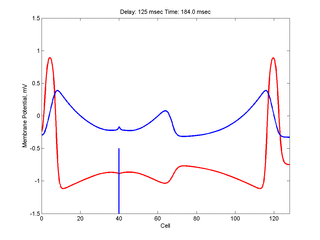
Putting it all together: Dynamic vulnerability and a propagating front
The timing of the test (s2) stimulus is critical relative to the conditioning stimulus (s1). If the s1-s2 delay is short, the inhibitory current (blue) is large rendering the medium inexcitable. If, on the other hand, the s1-s2 delay is too long, then the medium will have fully recovered its excitability. Shown here is an s1-s2 delay (125 msec), timed to occur as the vulnerable region passes over the s2 stimulation site. For this example, the blue line at cell 40 is the test stimulation site. With a properly timed test stimulus, the inhibitory current (blue) is near its rest value (medium is fully excitable) and the gradient of excitability is such that the retrograde wave propagates (away from the conditioning wave) while the antigrade wave decrementally propagates and eventually collapses as shown here.
Stimulation pulse initial conditions as an approximation of the stationary wave
Question: What is the amplitude and width of a rectangular pulse such that the IC does not collapse to a stationary wave. What is the minimum amplitude of a rectangular pulse such that it does not grow but collapses?
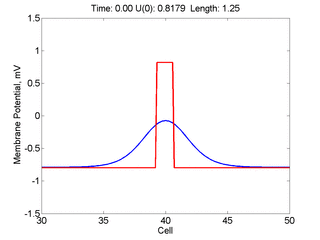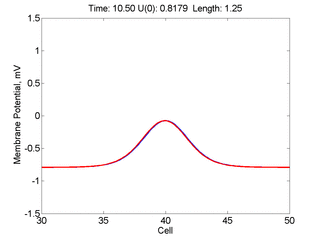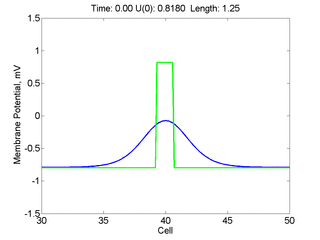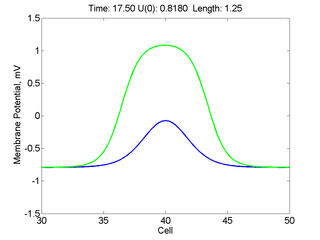
Instead of varying the duration of a stimulus pulse, the length of the stimulus electrode can be varied. Below is an interesting demonstration of the dynamic response of the medium to the interaction between the length of the stimulus electrode and the amplitude of the stimulus pulse. Instead of a stimulus pulse, here I simply specify the initial condition for the cable - either a short high amplitude initial condition or a longer, low amplitude initial condition. I then change the amplitude slightly to illustrate the fate of the initial condition when a region slightly greater than (green) the critical nucleus is excited or a region slightly less than (red) the critical nucleus is excited.
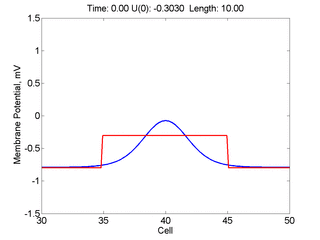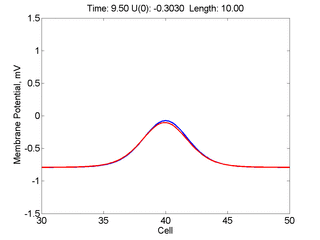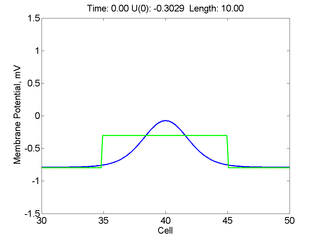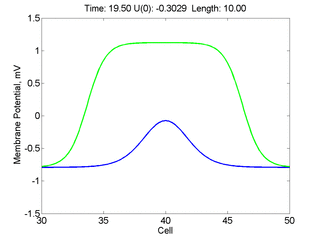
For me, to observe that pulse initial condition collapses to a profile that approximates the critical nucleus was a surprise and that small static gradients of excitability might demonstrate stationary vulnerability. On the left, the success of propagation depends on the amplitude. The red pulse has an amplitude of 0.8179 and collapses while the blue curve has an amplitude of 0.8180 and propagates. In either case, the initial pulse collapses to that approximating the critical nucleus. For a longer width excited region, the same dynamics is observed. An initial amplitude of -0.3030 (red) collapses while a slightly more positive amplitude of -0.3029 expands and propagates. The blue curve is the theoretical critical nucleus.
Follow-up (2014) - Lucia Romera in Valencia made a very insightful study into the safety factor and stationary waves. See Non-Uniform Dispersion of the Source-Sink Relationship Alters Wavefront Curvature PLOS|One

This work is licensed under a Creative Commons License.
C. Frank Starmer