|
|




Next: Properties of
Up: Linear Models
Previous: Setting up Y and
Index
Click for printer friendely version of this HowTo
Parameter Estimation:
The Least Squares Method
Given data for the dependent and independent variables, X and
Y, how should
we estimate the values for
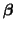 , the model parameters?
For this we can use the least
squares procedure. That is, estimate , the model parameters?
For this we can use the least
squares procedure. That is, estimate
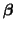 by
minimizing the total squared differences
between observed and predicted values. The difference between the
observed and predicted values, often times called the residual,
is, in matrix notation, by
minimizing the total squared differences
between observed and predicted values. The difference between the
observed and predicted values, often times called the residual,
is, in matrix notation,
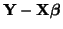 . The squared residual is . The squared residual is
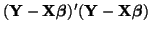 . Thus, . Thus,
To minimize Equation 3.13.4, we take its derivative with
respect to
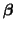 , set it equal to zero and solve for , set it equal to zero and solve for
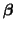 . .
and thus3.14
![$\displaystyle \boldsymbol{\hat{\beta}} = \mathbf{[X'X]^{-1}X'Y}.$](img787.png) |
(3.13.5) |
If we substitute our estimated parameters,
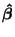 , into Equation 3.13.4, we
get the following simplification for calculating the squared residual: , into Equation 3.13.4, we
get the following simplification for calculating the squared residual:




Next: Properties of
Up: Linear Models
Previous: Setting up Y and
Index
Click for printer friendely version of this HowTo
Frank Starmer
2004-05-19
| |